2023-2024学年冀教版初中数学九年级下册 29.5 正多边形与圆同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 正六边形内接于圆,它的边所对的圆周角是( )A、60° B、120° C、60°或120° D、30°或150°2. 如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
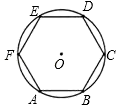 A、 B、 C、 D、3. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和的长分别为( )
A、 B、 C、 D、3. 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和的长分别为( ) A、 , π B、 , π C、 , D、 , 2π4. 如图所示,正五边形ABCDE内接于为BC的中点,为DE的中点,则的大小为( ).
A、 , π B、 , π C、 , D、 , 2π4. 如图所示,正五边形ABCDE内接于为BC的中点,为DE的中点,则的大小为( ). A、 B、 C、 D、5. 如图,在圆内接正六边形ABCDEF中,BF , BD分别交AC于点G , H , 若该圆的半径为12,则线段GH的长为( )
A、 B、 C、 D、5. 如图,在圆内接正六边形ABCDEF中,BF , BD分别交AC于点G , H , 若该圆的半径为12,则线段GH的长为( )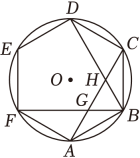 A、6 B、 C、 D、86. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).
A、6 B、 C、 D、86. 如图,四边形ABCD是⊙O的内接正方形,正方形PQRS的顶点S,R在⊙O上,则S正方形PQRS:S正方形ABCD等于( ).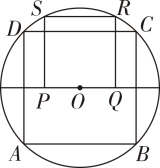 A、1 :2 B、1:3 C、2:3 D、2:57. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )
A、1 :2 B、1:3 C、2:3 D、2:57. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )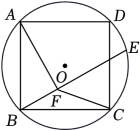 A、 B、1 C、 D、8. 如图,将的圆周分成五等分(分点为A、B、C、D、E),依次隔一个分点相连,即成一个正五角星形.小张在制图过程中,惊讶于图形的奇妙,于是对图形展开了研究,得到:点M是线段AD、BE的黄金分割点,也是线段NE、AH的黄金分割点.在以下结论中,不正确的是( )
A、 B、1 C、 D、8. 如图,将的圆周分成五等分(分点为A、B、C、D、E),依次隔一个分点相连,即成一个正五角星形.小张在制图过程中,惊讶于图形的奇妙,于是对图形展开了研究,得到:点M是线段AD、BE的黄金分割点,也是线段NE、AH的黄金分割点.在以下结论中,不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
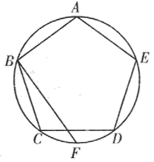
9. 如图,正五边形 内接于 ,F是 的中点,则 的度数为.
 10. 如图, 等边三角形ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,则⊙O的半径R为
10. 如图, 等边三角形ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,则⊙O的半径R为 11. 同一个圆的内接正三角形、正方形、正六边形的边心距(内接圆的圆心到正多边形的边的距离)之比为.12. 如图,边长为6的正方形内接于 , 点E是上的一动点(不与A , B重合,点F是上的一点,连接 , 分别与交于点G , H , 且 , 有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是.(填序号)
11. 同一个圆的内接正三角形、正方形、正六边形的边心距(内接圆的圆心到正多边形的边的距离)之比为.12. 如图,边长为6的正方形内接于 , 点E是上的一动点(不与A , B重合,点F是上的一点,连接 , 分别与交于点G , H , 且 , 有以下结论:①;②周长的最小值为;③随着点E位置的变化,四边形的面积始终为9.其中正确的是.(填序号)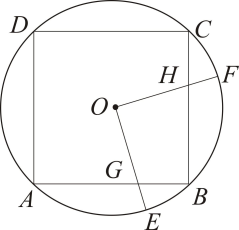 13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
三、解答题
-
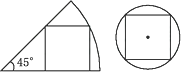
14. 一张圆心角为45°的扇形纸板和圆形纸板按如图方式各剪得一个正方形,边长都为1,求扇形纸板和圆形纸板的面积比.
 15. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).
15. 如图,正方形ABCD的外接圆为⊙O,点P在劣弧 上(不与C点重合).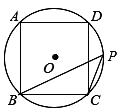 (1)、求∠BPC的度数;
(1)、求∠BPC的度数;
(2)、若⊙O的半径为8,求正方形ABCD的边长.四、综合题
-
16. 如图,正六边形ABCDEF的对称中心P在反比例函数y= (k>0,x>0)的图象上边CD在x轴上,点B在y轴上,已知CD=4.
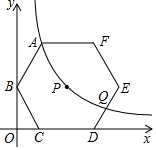 (1)、点A是否在该反比例函数的图象上?请说明理由.
(1)、点A是否在该反比例函数的图象上?请说明理由.
(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标;
(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
17. 阅读下列材料,并按要求完成相应的任务.黄金三角形与五角星
当等腰三角形的顶角为36°(或108°)时,它的底与腰的比(或腰与底的比)为 , 我们把这样的三角形叫做黄金三角形.
按下面的步骤画一个五角星(如图):
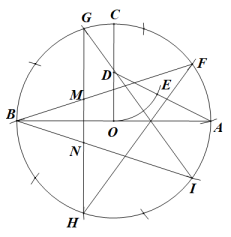
①作一个以AB为直径的圆,圆心为O;
②过圆心O作半径OC⊥AB;
③取OC的中点D,连接AD;
④以D为圆心OD为半径画弧交AD于点E;
⑤从点A开始以AE为半径顺时针依次画弧,
正好把⊙O十等分(其中点F,G,B,H,I为五等分点);
⑥以点F,G,B,H,I为顶点画出五角星.
任务:
(1)、求出的值为;(2)、如图,GH与BF,BI分别交于点M,N,求证:△BMN是黄金三角形.