2023-2024学年冀教版初中数学九年级下册 29.3 切线的性质与判定同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,点O是外接圆的圆心,点I是的内心,连接 , . 若 , 则的度数为( )
 A、 B、 C、 D、2. 如图,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A、B两点的切线交于点C , 测得 , A , B两点之间的距离为72米。则这段公路AB的长度为( )
A、 B、 C、 D、2. 如图,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A、B两点的切线交于点C , 测得 , A , B两点之间的距离为72米。则这段公路AB的长度为( ) A、12π米 B、24π米 C、36π米 D、48π米3. 题目:“如图,在等腰直角三角形中, , 以点为圆心,以小于的长度为半径作 , 是上一点,连接 . 将线役绕点顺时针旋转得到线段 , 连接 . 当为何度数时,与相切,切点为?”对于其答案,甲答: , 乙答: , 丙答: , 则下列判断正确的是( )
A、12π米 B、24π米 C、36π米 D、48π米3. 题目:“如图,在等腰直角三角形中, , 以点为圆心,以小于的长度为半径作 , 是上一点,连接 . 将线役绕点顺时针旋转得到线段 , 连接 . 当为何度数时,与相切,切点为?”对于其答案,甲答: , 乙答: , 丙答: , 则下列判断正确的是( ) A、只有甲答的对 B、甲、丙答案合在一起才完整 C、乙、丙答案合在一起才完整 D、三人答案合在一起才完整4. 如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )
A、只有甲答的对 B、甲、丙答案合在一起才完整 C、乙、丙答案合在一起才完整 D、三人答案合在一起才完整4. 如图,已知△ABC,AB=BC,以AB为直径的圆交AC于点D,过点D的⊙O的切线交BC于点E.若CD=5,CE=4,则⊙O的半径是( )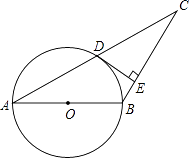 A、3 B、4 C、 D、5. 如图,正方形 的顶点A、D在⊙O上,边 与⊙O相切,若正方形 的周长记为 ,⊙O的周长记为 ,则 、 的大小关系为( )
A、3 B、4 C、 D、5. 如图,正方形 的顶点A、D在⊙O上,边 与⊙O相切,若正方形 的周长记为 ,⊙O的周长记为 ,则 、 的大小关系为( ) A、 B、 C、 D、无法判断6. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )
A、 B、 C、 D、无法判断6. 如图,一个零刻度落在点A的量角器(半圆O),其直径为AB , 一等腰直角三角板MNB绕点B旋转,斜边BN交半圆O于点C , BM交半圆O于点D , 点C在量角器上的读数为.关于结论Ⅰ,Ⅱ,下列判断正确的是( )结论Ⅰ:;
结论Ⅱ:当边MN与半圆O相切于点E(点E在量角器上的读数为)时,
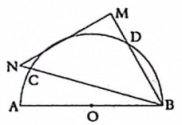 A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对7. 如图,正比例函数与反比例函数的图象相交于A、B两点,分别以A、B两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( )
A、只有结论Ⅰ对 B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对7. 如图,正比例函数与反比例函数的图象相交于A、B两点,分别以A、B两点为圆心,画与x轴相切的两个圆,若点A的坐标为(2,1),则图中两个阴影部分面积的和是( ) A、 B、 C、π D、4π8. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )
A、 B、 C、π D、4π8. 如图,是的内切圆, , 过点I作分别交 , 于N,M,若 , , 则的半径是( )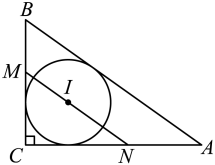 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,边长为的正方形内接于 , 分别过点A , D作的切线,两条切线交于点P , 则图中阴影部分的面积是.
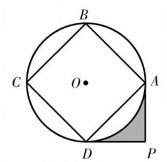 10. 如图,在△ABC中,AC=BC , ∠ACB=100°,⊙O与AB , BC分别切于点D , C , 连接CD . 则∠ACD的度数为 .
10. 如图,在△ABC中,AC=BC , ∠ACB=100°,⊙O与AB , BC分别切于点D , C , 连接CD . 则∠ACD的度数为 . 11. 如图,PA , PB分别与⊙O相切于A , B , CE切⊙O于E , 已知PO=13cm , ⊙O的半径为5cm , 则△PDE的周长是 cm .
11. 如图,PA , PB分别与⊙O相切于A , B , CE切⊙O于E , 已知PO=13cm , ⊙O的半径为5cm , 则△PDE的周长是 cm . 12. 如图,在矩形中, , 点分别是边上的两点,连接 , 以为直径的半圆分别与矩形的另外两边相切,则图中阴影部分的周长为(结果保留)
12. 如图,在矩形中, , 点分别是边上的两点,连接 , 以为直径的半圆分别与矩形的另外两边相切,则图中阴影部分的周长为(结果保留) 13. 如图,在中. , . 是的内切圆.分别与 , , 相切于点 , , .
13. 如图,在中. , . 是的内切圆.分别与 , , 相切于点 , , . (1)、 .(2)、若 , 则 .
(1)、 .(2)、若 , 则 .三、解答题
-
14. 如图1,已知AB是的直径,且 , BM切于点B , 点P是上的一个动点(不经过A , B两点),连接PA , 过点O作交BM于点Q , 过点P作于点C , 交QO的延长线于点E , 连接AE , PQ.
图1
 (备用图)
(备用图) (1)、求证:;(2)、试判断PQ与的位置关系,并给予证明;(3)、随着点P的移动,四边形PAEO能否为菱形,若能,请说明点E与的位置关系,并求出PE的长;若不能,请说明理由.15. 在中, , 以为直径的分别与交于点 , 过点作于点 .
(1)、求证:;(2)、试判断PQ与的位置关系,并给予证明;(3)、随着点P的移动,四边形PAEO能否为菱形,若能,请说明点E与的位置关系,并求出PE的长;若不能,请说明理由.15. 在中, , 以为直径的分别与交于点 , 过点作于点 . (1)、求证:是的切线;(2)、如图1,若的半径为 , 求阴影部分的面积;(3)、如图2,若 , 求的值.
(1)、求证:是的切线;(2)、如图1,若的半径为 , 求阴影部分的面积;(3)、如图2,若 , 求的值.四、综合题
-
16. 如图,在中, , 以为直径的与交于点D,点是的中点,连接 , .
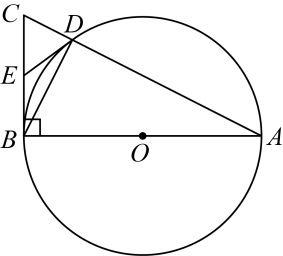 (1)、求证:是的切线;(2)、若 , , 求的长;(3)、在(2)的条件下,点P是上一动点,求的最大值.17. 如图1,菱形ABCD中,∠DAB=60°,AB=4.点P为射线AB上一动点,在射线DA上取一点E , 连接DP , EP , 使∠DPE=60°.作△APE的外接圆,设圆心为O.
(1)、求证:是的切线;(2)、若 , , 求的长;(3)、在(2)的条件下,点P是上一动点,求的最大值.17. 如图1,菱形ABCD中,∠DAB=60°,AB=4.点P为射线AB上一动点,在射线DA上取一点E , 连接DP , EP , 使∠DPE=60°.作△APE的外接圆,设圆心为O. (1)、当圆心O在AB上时,AE=;(2)、当点E在边AD上时,
(1)、当圆心O在AB上时,AE=;(2)、当点E在边AD上时,①判断⊙O与DP的位置关系,并证明;
②当AP为何值时,AE有最大值?并求出最大值;
(3)、如图2,连接AC , 若PE∥AC , 则AP=;将优弧PE沿PE翻折交射线AC于点Q , 则PQ的弧长=.