冀教版初中数学九年级下册 29.2 直线与圆的位置关系同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 已知的直径为10,直线l与相交,则圆心O到直线l的距离可能是( )A、4 B、5 C、6 D、82. 已知圆与直线有两个公共点,且圆心到直线的距离为4,则该圆的半径可能为( )A、2 B、3 C、4 D、53. 已知中, , 、 . 以C为圆心作 , 如果圆C与斜边有两个公共点,那么圆C的半径长R的取值范围是( )A、 B、 C、 D、 .4. 若的半径为3,圆心到直线l的距离为3,那么直线与的位置关系是( )A、相离 B、相切 C、相交 D、不能确定5. 如图,在Rt△ABC中,∠C=90°,BC=18,AC=24,点O在边AB上,且BO=2OA . 以点O为圆心,r为半径作圆,如果⊙O与Rt△ABC的边有3个公共点,那么下列各值中,半径r不可以取的是( )
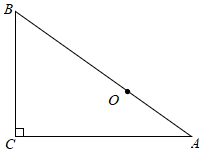 A、6 B、10 C、15 D、166. 如图,已知 两点的坐标分别为 ,点 分别是直线 和x轴上的动点, ,点D是线段 的中点,连接 交y轴于点E;当⊿ 面积取得最小值时, 的值是( )
A、6 B、10 C、15 D、166. 如图,已知 两点的坐标分别为 ,点 分别是直线 和x轴上的动点, ,点D是线段 的中点,连接 交y轴于点E;当⊿ 面积取得最小值时, 的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 已知,⊙O的半径为一元二次方程x2﹣5x﹣6=0的两根,圆心O到直线l的距离d=4,则直线l与⊙O的位置关系是 .8. ⊙O的半径为5cm,点O到直线AB的距离为d,当d=时,AB与⊙O相切.9. 已知 , 、之间的距离是5cm,圆心O到直线的距离是2cm,如果圆O与直线、有三个公共点,那么圆O的半径为cm.10. 如图,在矩形中, , , 点E是的中点,连接 , 点O是线段上一点,的半径为1,如果与矩形的各边都没有公共点,那么线段长的取值范围是 .
 11. 如图,半圆的圆心与坐标原点重合,半圆的半径为2,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是.
11. 如图,半圆的圆心与坐标原点重合,半圆的半径为2,直线l的解析式为y=x+t.若直线l与半圆只有一个交点,则t的取值范围是.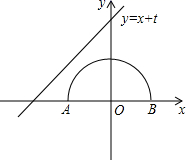
三、解答题
-
12. 如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD= , 点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
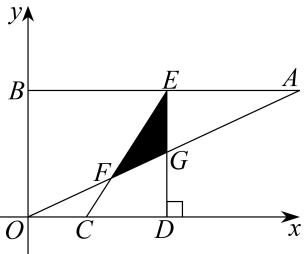
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有DF=CD?
②直接写出ΔCDF的外接圆与OA相切时t的值.13. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.(Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).

四、综合题
-
14. 对于平面直角坐标系内的点和图形 , 给出如下定义:如果点绕原点顺时针旋转得到点 , 点落在图形上或图形围成的区域内,那么称点是图形关于原点的“伴随点”.(1)、已知点 , , . ①在点 , , 中,点 ▲ 是线段关于原点的“伴随点”;②如果点是关于原点的“伴随点”,求的取值范围;(2)、的圆心坐标为 , 半径为1,如果直线上存在关于原点的“伴随点”,直接写出的取值范围.15. 如图,是的直径, , 是的弦,且 , 垂足为 , 连接 , 过点作的切线,交的延长线于点 .
 (1)、求证:;(2)、若点是的中点,且 , 求线段的长;(3)、在(2)的情况下,求阴影部分的面积.
(1)、求证:;(2)、若点是的中点,且 , 求线段的长;(3)、在(2)的情况下,求阴影部分的面积.