2023-2024学年冀教版初中数学九年级下册 29.1 点与圆的位置关系同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如果⊙O的半径为6，线段OP的长为3，则点P与⊙O的位置关系是（　　）

A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O外 D、无法确定

查看试题解析
2. 已知⊙O的半径为5cm ，点A到圆心O的距离为6cm ，则点A与⊙O的位置关系为（）

A、点A在⊙O上 B、点A在⊙O内 C、点A在⊙O外 D、不能确定

查看试题解析
3. 如图，已知 $⊙ O$ 及其所在平面内的4个点．如果 $⊙ O$ 半径为5，那么到圆心 $O$ 距离为7的点可能是（）

A、 $P$ 点 B、 $Q$ 点 C、 $M$ 点 D、 $N$ 点

查看试题解析
4. 如图，在 $5 \times 5$ 的正方形网格中（小正方形的连长为1），有6个点A、B、C、D、E、F，若过A、B、C三点作圆O，则点D、E、F三点中在圆O外的有（）个

A、0 B、1 C、2 D、3

查看试题解析
5. 如图， $∠ M O N = 45 °$ ，点A、B分别在射线 $O M$ 、射线 $O N$ 上运动，四边形 $A B C D$ 是矩形，且 $A B = 2$ ， $A D = 1$ ，则 $O D$ 的最大值为（）

A、 $\sqrt{2} + \sqrt{5}$ B、 $2 \sqrt{2} + 1$ C、 $\sqrt{2} + \sqrt{3}$ D、无最大值

查看试题解析
6. 如图，四边形ABCD为矩形，AB＝3，BC＝4，点P是线段BC上一动点，点M为线段AP上一点，∠ADM＝∠BAP，则BM的最小值为（）

A、 $\frac{5}{2}$ B、 $\frac{12}{5}$ C、 $\sqrt{13}$ - $\frac{3}{2}$ D、 $\sqrt{13}$ -2

查看试题解析
7. 已知P(x，y)是以坐标原点为圆心，5为半径的圆周上的点，若x，y都是整数，则这样的点共有（）

A、4个 B、8个 C、12个 D、16个

查看试题解析
8. 如图，在6×6的正方形网格图形 $A B C D$ 中，M，N分别是 $A B ， B C$ 上的格点， $B M = 4 ， B N = 2$ .若点P是这个网格图形中的格点，连接PM，PN，则所有满足 $∠ M P N = 45 °$ 的 $△ P M N$ 中， $D P$ 的最小值是（）

A、 $3 \sqrt{2} - \sqrt{10}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

9. 已知⊙O的半径为4cm，OP =2cm，则点P在⊙O（填“内"、“外”或“上”）．

查看试题解析
10. 在 $△ A B C$ 中， $∠ A B C = 9 0^{°} ， A B = 2 ， B C = 3 . D$ 为平面上一个动点， $∠ A D B$ $= 4 5^{°}$ ，则线段CD的长度的最小值为.

查看试题解析
11. ⊙O外一点P到⊙O上的点的最大距离是12，最小距离是2，求此圆的半径是

查看试题解析
12. 如图，AB是半圆O的直径，点C在半圆O上，AB＝4，∠CAB＝60°，P是弧BC上的一个动点，连结AP，过点C点作CD⊥AP于点D，连结BD，在点P移动的过程中.

(1)、AC＝；

(2)、BD的最小值是.

查看试题解析
13. 如图，线段 $A B$ 为 $⊙ O$ 的直径，点C在 $A B$ 的延长线上， $A B = 4$ ， $B C = 2$ ，点P是 $⊙ O$ 上一动点，连接 $C P$ ，以 $C P$ 为斜边在 $P C$ 的上方作Rt $△ P C D$ ，且使 $∠ D C P = 60 °$ ，连接 $O D$ ，则 $O D$ 长的最大值为．

查看试题解析

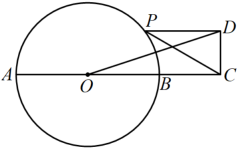
三、解答题

14. 如图，A城气象台测得一热带风暴中心O从A城正西方向300km处向东北方向移动，距风暴中心200km的范围内为受影响区域．问：A城是否会受到这次热带风暴的影响？请说明理由．

查看试题解析
15.
如图，在Rt△ABC中，∠ABC=90°，点F为AC中点，⊙O经过点B，F，且与AC交于点D，与AB交于点E，与BC交于点G，连结BF，DE，弧EFG的长度为（1+ $\frac{\sqrt{3}}{2}$ ）π．
（1）求⊙O的半径；
（2）若DE∥BF，且AE=a，DF=2+ $\sqrt{3}$ ﹣a，请判断圆心O和直线BF的位置关系，并说明理由．

查看试题解析

四、综合题

16. 如图1，在矩形ABCD中， $A B = 4$ ， $B C = 6$ .点E是线段AD上的动点（点E不与点A，D重合），连接CE，过点E作 $E F ⊥ C E$ ，交AB于点F.

(1)、求证： $△ A E F ∽ △ D C E$ ；

(2)、如图2，连接CF，过点B作 $B G ⊥ C F$ ，垂足为G，连接AG.点M是线段BC的中点，连接GM.
①求 $A G + G M$ 的最小值；

②当 $A G + G M$ 取最小值时，求线段DE的长.

查看试题解析
17. 如图1，在矩形ABCD中，E、F、G分别为边BC、AB、AD的中点，连接DF、EF，H为DF中点，连接GH，将 $△ B E F$ 绕点B旋转.

(1)、当 $△ B E F$ 旋转到如图2的位置，连接AF、CE，若 $A B = B C$ ，且 $C E = 2$ ，则 $A F =$ ， $G H =$ ；

(2)、已知 $A B = 3 ， B C = 4$ .
①当 $△ B E F$ 旋转到如图3位置时，连接CE，猜想GH与CE之间的数量关系和位置关系，并说明理由.
②在 $△ B E F$ 旋转过程中，射线GH，CE相交于点Q，连接AQ，AQ有最小值吗？若有，请直接写出AQ的最小值；若没有，请说明理由.

查看试题解析