2023-2024学年冀教版初中数学八年级下册 19.2 平面直角坐标系同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 若点P(x,y)是第四象限内的点,且点P到x轴的距离为2,到y轴的距离为3,则P点的坐标是( )A、(3,2) B、(-2,3) C、(2,-3) D、(3,-2)2. 点A(x,y)满足二元一次方程组的解,则点A在第( )象限.A、一 B、二 C、三 D、四3. 如图,在平面直角坐标系xOy中,被一团墨水覆盖住的点的坐标有可能是( )
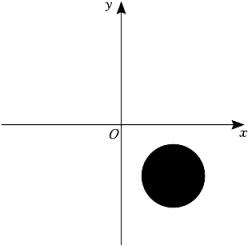 A、(2,-4) B、(-2,4) C、(-2,-4) D、(2,4)4. 课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,1)表示,小军的位置用(2,2)表示,那么你的位置可以表示成( )”
A、(2,-4) B、(-2,4) C、(-2,-4) D、(2,4)4. 课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,1)表示,小军的位置用(2,2)表示,那么你的位置可以表示成( )” A、(5,4) B、(4,5) C、(4,4) D、(4,3)5. 已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、-3 B、-5 C、1或-3 D、1或-56. 在平面直角坐标系中,对于点 , 若点坐标为其中为常数,且 , 则称点是点的“属派生点”例如,点的“属派生点”为 , 即若点的“属派生点是点 , 则点的坐标为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点 , , , , …,那么点的坐标为( )
A、(5,4) B、(4,5) C、(4,4) D、(4,3)5. 已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、-3 B、-5 C、1或-3 D、1或-56. 在平面直角坐标系中,对于点 , 若点坐标为其中为常数,且 , 则称点是点的“属派生点”例如,点的“属派生点”为 , 即若点的“属派生点是点 , 则点的坐标为( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次平移,每次移动一个单位,得到点 , , , , …,那么点的坐标为( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,点的坐标为 . 线段以每秒旋转90°的速度,绕点沿顺时针方向连续旋转,同时,点从点出发,以每秒移动1个单位长度的速度,在线段上,按照…的路线循环运动,则第2023秒时点的坐标为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点的坐标为 . 线段以每秒旋转90°的速度,绕点沿顺时针方向连续旋转,同时,点从点出发,以每秒移动1个单位长度的速度,在线段上,按照…的路线循环运动,则第2023秒时点的坐标为( )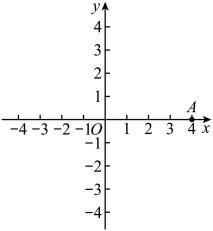 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
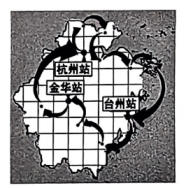
9. 平面直角坐标系中,若点A在第二象限,且到x轴的距离为3,到y轴的距离为2,则点A的坐标为 .10. 如图是杭州第19届亚运会火炬传递路线示意图.若以“杭州站”为原点建立平面直角坐标系,“金华站”的坐标可表示为 , 则“台州站”的坐标可表示为.
 11. 已知点A(3a-9,2-a)关于原点对称的点为A′,点A′关于x轴对称的点为A″,点A″在第四象限,那么a的取值范围是 .12. 如图所示,在平面直角坐标系中,动点按图中箭头所示方向依次运动,第1次运动到点 , 第2次运动到点 , 第3次运动到点 , 第4次运动到点 , 按这样的运动规律,动点第2023次运动到点的坐标为 .
11. 已知点A(3a-9,2-a)关于原点对称的点为A′,点A′关于x轴对称的点为A″,点A″在第四象限,那么a的取值范围是 .12. 如图所示,在平面直角坐标系中,动点按图中箭头所示方向依次运动,第1次运动到点 , 第2次运动到点 , 第3次运动到点 , 第4次运动到点 , 按这样的运动规律,动点第2023次运动到点的坐标为 . 13. 如图,在平面直角坐标系中,点 , 点第次向上跳动个单位至点 , 紧接着第次向右跳动个单位至点 , 第次向上跳动个单位,第次向左跳动个单位,第次又向上跳动个单位,第次向右跳动个单位,依此规律跳动下去,点第次跳动至点的坐标是 .
13. 如图,在平面直角坐标系中,点 , 点第次向上跳动个单位至点 , 紧接着第次向右跳动个单位至点 , 第次向上跳动个单位,第次向左跳动个单位,第次又向上跳动个单位,第次向右跳动个单位,依此规律跳动下去,点第次跳动至点的坐标是 .
三、解答题
-
14. 已知点P(x , y)的坐标满足方程组 , 点P在第三象限.(1)、请用含a的代表式表示x;(2)、请求出a的取值范围.15. 若点的坐标满足 .(1)、若点的坐标为 , 求 , 的值;(2)、若点在第二象限,且符合要求的整数只有五个,求的取值范围;(3)、若点为不在轴上的点,且关于的不等式的解集为 , 求关于的不等式的解集.
四、综合题
-
16. 在平面直角坐标系中,对于点 , 若点Q的坐标为 , 其中a为常数,则称点Q是点P的“a级关联点”.(1)、已知点的“级关联点”是点 , 则点的坐标为;(2)、已知点的“级关联点”N位于x轴上,求点N的坐标;(3)、在(2)的条件下,若存在点H , 使轴,且 , 直接写出H点坐标.