2023-2024学年冀教版初中数学八年级下册 19.2 平面直角坐标系同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 已知点A的坐标为(a+1,3﹣a),下列说法正确的是( )A、若点A在y轴上,则a=3 B、若点A在一三象限角平分线上,则a=1 C、若点A到x轴的距离是3,则a=±6 D、若点A在第四象限,则a的值可以为﹣22. 在平面直角坐标系中,点位于第三象限,则( )A、 B、 C、 D、3. 在平面直角坐标系中,点到轴的距离是( )A、4 B、3 C、 D、4. 已知a+b>0,ab>0,如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
 A、(a,b) B、(-a,b) C、(-a,-b) D、(a,-b)5. 已知点 , 若 , , 则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,是象棋盘的一部分,若“帅”位于点 , “相”位于点上,则“炮”位于点( )上.
A、(a,b) B、(-a,b) C、(-a,-b) D、(a,-b)5. 已知点 , 若 , , 则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,是象棋盘的一部分,若“帅”位于点 , “相”位于点上,则“炮”位于点( )上.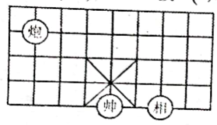 A、 B、 C、 D、7. 在平面直角坐标系中,点A的坐标为 , 则点A到x轴距离为( )A、 B、5 C、 D、28. 如图,在平面直角坐标系中点A、B、C的坐标分别为(0,1),(3,1),(4,3),在下列选项的E点坐标中,不能使△ABE和△ABC全等是( )
A、 B、 C、 D、7. 在平面直角坐标系中,点A的坐标为 , 则点A到x轴距离为( )A、 B、5 C、 D、28. 如图,在平面直角坐标系中点A、B、C的坐标分别为(0,1),(3,1),(4,3),在下列选项的E点坐标中,不能使△ABE和△ABC全等是( ) A、(4,﹣1) B、(﹣1,3) C、(﹣1,﹣1) D、(1,3)
A、(4,﹣1) B、(﹣1,3) C、(﹣1,﹣1) D、(1,3)二、填空题
-
9. 在平面直角坐标系中,直线平行于y轴.若点A的坐标为 , 则点B的坐标可以是 . (写出一个即可)10. 在平面直角坐标系中,点到轴的距离是11. 如图,在“笑脸”的“嘴巴”上找一格点,这一格点的坐标可以为(写出一点即可).
 12. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , 则内部的格点个数是 .
12. 皮克定理是格点几何学中的一个重要定理,它揭示了以格点为顶点的多边形的面积 , 其中分别表示这个多边形内部与边界上的格点个数.在平面直角坐标系中,横、纵坐标都是整数的点为格点.已知 , 则内部的格点个数是 .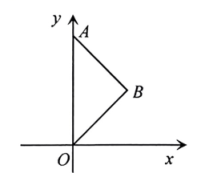 13. 如图,在直角坐标系中,长方形的顶点分别在轴,轴上,点的坐标分别为为边上一点,点的坐标为 , 若是腰长为5的等腰三角形,则点的坐标是 .
13. 如图,在直角坐标系中,长方形的顶点分别在轴,轴上,点的坐标分别为为边上一点,点的坐标为 , 若是腰长为5的等腰三角形,则点的坐标是 .
三、解答题
-
14. 已知点 , 解答下列各题:(1)、点在轴上,求出点的坐标;(2)、若点在第二象限,且它到轴的距离与轴的距离相等,求的值.15. 围棋,起源于中国,古代称为“弈”,是棋类鼻祖,距今已有4000多年的历史.如图是某围棋棋盘的一部分,若棋盘是由边长均为1的小正方形组成的,棋盘上两颗棋子的坐标分别为 .
 (1)、根据题意,画出相应的平面直角坐标系;(2)、有一颗黑色棋子的坐标为 , 请标注出黑色棋子的位置.
(1)、根据题意,画出相应的平面直角坐标系;(2)、有一颗黑色棋子的坐标为 , 请标注出黑色棋子的位置.四、综合题
-
16. 在平面直角坐标系中,点是坐标原点,点的坐标是 , 点的坐标是 , 且 , , 满足 .(1)、若为不等式的最大整数解,判断点在第几象限,说明理由;(2)、求点的坐标;(3)、若有两个动点、 , 请探索是否存在以两个动点、为端点的线段 , 且 , 若存在,求、两点的坐标;若不存在,请说明理由.