2023-2024学年冀教版初中数学八年级下册 19.1 确认平面上物体的位置同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如图在正方形网格中，若A（1，1），B（2，0），则C点的坐标为（）

A、（﹣3，﹣2） B、（3，﹣2） C、（﹣2，﹣3） D、（2，﹣3）

查看试题解析
2. 学校在李老师家的南偏东 $4 0^{°}$ 方向，距离是 $800 m$ ，则李老师家在学校的（）

A、北偏东 $4 0^{°}$ 方向，相距 $800 m$ 处 B、北偏西 $4 0^{°}$ 方向，相距 $800 m$ 处 C、北偏东 $5 0^{°}$ 方向，相距 $800 m$ 处 D、北偏西 $5 0^{°}$ 方向，相距 $800 m$ 处

查看试题解析
3. 课间操时，小华、小军、小刚的位置如图．小华对小刚说：“如果我的位置用 $(0 ， 0)$ 表示，小军的位置用 $(2 ， 1)$ 表示，那么你的位置可以表示成（）

A、 $(5 ， 4)$ B、 $(4 ， 5)$ C、 $(3 ， 4)$ D、 $(4 ， 3)$

查看试题解析
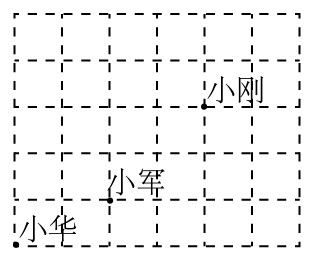4. 观察如图所示的象棋棋盘， $(5 ， 1)$ 表示“帅”的位置，马走“日”字，那么“马8进7”（即第8列的马前进到第7列）后的位置可表示为（）

A、 $(7 ， 5)$ B、 $(5 ， 7)$ C、 $(7 ， 2)$ D、 $(2 ， 7)$

查看试题解析
5. 如图是一轰炸机群的飞行队形示意图，若在图上建立平面直角坐标，使最后两架轰炸机分别位于点 $M (- 1 ， 1)$ 和点 $N (- 1 ， - 3)$ ，则第一架轰炸机位于的点P的坐标是（）

A、 $(3 ， - 1)$ B、 $(- 1 ， 3)$ C、 $(- 3 ， - 1)$ D、 $(3 ， 0)$

查看试题解析
6. 某天课间操时，嘉嘉、淇淇、小高的位置如图所示，嘉嘉对小高说：“如果我的位置用 $(0 ， 0)$ 表示，淇淇的位置用 $(6 ， 2)$ 表示，那么你的位置可以表示成什么？”（）

A、 $(8 ， 3)$ B、 $(3 ， 8)$ C、 $(7 ， 4)$ D、 $(8 ， 4)$

查看试题解析
7. 在一次“寻宝”游戏中，寻宝人已经找到两个标志点 $A (2 ， 3)$ 和 $B (1 ， - 1)$ ，并且知道藏宝地点的坐标是 $(3 ， 2)$ ，则藏宝处应为图中的（）

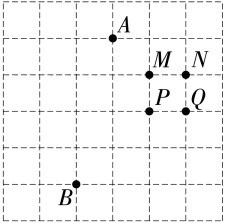A、点 $M$ B、点 $N$ C、点 $P$ D、点 $Q$

查看试题解析
8. 小明家位于公园的正东方向500m处，从小明家出发向北走600m就到小华家.若选取小华家所在位置为原点，分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系，则公园的坐标是（）

A、（－600，－500） B、（500，600） C、（－500，－600） D、（600，500）

查看试题解析

二、填空题

9. 在平面内取一个定点 $O$ ，叫极点，引一条射线 $O x$ ，叫做极轴，再选定一个长度单位和角度的正方向 $($ 通常取逆时针方向 $) .$ 对于平面内任何一点 $M$ ，用 $ρ$ 表示线段 $O M$ 的长度， $θ$ 表示从 $O x$ 到 $O M$ 的角度， $ρ$ 叫做点 $M$ 的极径， $θ$ 叫做点 $M$ 的极角，有序数对 $(ρ ， θ)$ 就叫点 $M$ 的极坐标，若 $O N ⊥ O X$ ，且点 $N$ 到极点 $O$ 的距离为 $4$ 个单位长度，则点 $N$ 的极坐标可表示为．

查看试题解析
10. 课间操时，小明、小丽、小亮的位置如图所示，如果小明的位置用 $(- 1 ， - 1)$ 表示，小丽的位置用 $(1 ， 0)$ 表示，那么小亮的位置可以表示成．

查看试题解析
11. 以水平数轴的原点 $O$ 为圆心，过正半轴 $O x$ 上的每一刻度点画同心圆，将 $O x$ 逆时针依次旋转 $30 °$ 、 $60 °$ 、 $90 °$ 、 $\dots$ 、 $330 °$ 得到 $11$ 条射线，构成如图所示的“圆”坐标系，点 $A$ 、 $B$ 的坐标分别表示为 $(5 ， 0 °)$ 、 $(4 ， 300 °)$ ，则点 $C$ 的坐标表示为．

查看试题解析
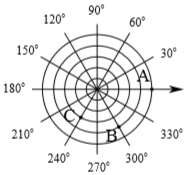12. 将交城卦山风景区中的半道亭，白塔，书院分别记为点A，B，C，若建立平面直角坐标系，将A，B用坐标表示为 $(2 ， 1)$ 和 $(8 ， 2)$ ，则书院C用坐标表示为．

查看试题解析

三、解答题

13. 小明家和学校所在地的简单地图如图所示，已知 $O A = 2 c m ， O B = 2.5 c m ， O P =$ $4 c m$ ，点 $C$ 为OP的中点，回答下列问题.

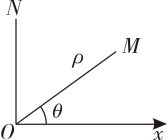
(1)、图中距小明家距离相同的是哪些地方?

(2)、写出学校、商场、公园、停车场相对于小明家的方位角，哪两个地方的方位角是相同的?

(3)、若学校距离小明家400m，那么商场和停车场分别距离小明家多少米?

查看试题解析
14. 如图1，将射线OX按逆时针方向旋转 $β$ 度，得到射线OY，如果点 $P$ 为射线OY上的一点，且 $O P = a$ ，那么我们规定用 $(a ， β)$ 表示点 $P$ 在平面内的位置，并记为 $P (a$ ， $β)$ .例如，图2中，如果 $O M = 8 ， ∠ X O M =$ $11 0^{°}$ ，那么点 $M$ 在平面内的位置记为 $M (8 ， 110)$ ，根据图形，解答下面的问题.

(1)、如图3，如果点 $N$ 在平面内的位置记为 $N (6 ， 30)$ ，那么 $O N =$ ， $∠ X O N =$ .

(2)、如果点A，B在平面内的位置分别记为 $A (5 ， 30) ， B (12 ， 120)$ ，试求A，B两点之间的距离并画出图形.

查看试题解析

四、综合题

15. 如图是某次海战中交战双方舰艇的对峙示意图，对甲方潜艇来说：

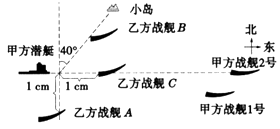(1)、北偏东40°的方向上有哪些目标？要想确定乙方战舰B的位置，还需要什么数据？

(2)、距甲方潜艇图上距离为1 cm处的乙舰有哪几艘？

(3)、要确定每艘乙舰的位置，各需几个数据？

查看试题解析
16. 如图是小丽以学校为观测点，画出的一张平面图．

(1)、生源大酒店在学校偏方向米处．汽车站在学校偏方向米处；

(2)、中医院在邮电局东偏北60°方向400米处，请在上图中标出它的位置；

(3)、小丽以每分钟50米的速度步行，从汽车站经过学校.邮局再到中医院大约需要分钟．

查看试题解析
17. 如图，蚂蚁在5×5的方格(每个小方格的边长均为1 cm)上沿着网格线运动．它从A处出发去寻找B，C，D处的伙伴，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向，那么图中：

(1)、A→D( ， )；D→B( ， )；C→B( ， )．

(2)、若蚂蚁的行走路线为A→B→C→D，请计算蚂蚁走过的路程．

(3)、若蚂蚁从A处出发去寻找伙伴，它的行走路线依次为(＋1，＋2)，(＋3，－1)，(－2，＋2)，请在图中标出这只蚂蚁伙伴的位置E.

(4)、在(3)中，若蚂蚁每走1 cm需要消耗1.5焦耳的能量，则蚂蚁在寻找伙伴E的过程中总共需要消耗多少焦耳的能量？

查看试题解析