2023-2024学年冀教版初中数学七年级下册 7.5 平行线的性质同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 命题:①两点之间线段最短;②对顶角相等;③同旁内角互补;④若一个角的两边与另一个角的两边互相平行,则这两个角一定相等;其中真命题有( )A、1个 B、2个 C、3个 D、4个2. 将一副常规直角三角板按如图所示的位置摆放在一把直尺上,则∠1的度数为( )
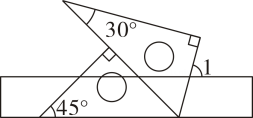 A、70 B、75 C、80 D、853. 下列说法中:①同位角相等;②点到直线的距离是指这点到直线的垂线段;③在同一平面内,若有一条直线a和一点A , 则过点A可以作两条直线AC和AB垂直于直线a;④过直线外一点有且只有一条直线与已知直线平行;⑤平移前后的两个图形的对应点连线一定平行.以上命题中真命题的个数是( )A、1个 B、2个 C、3个 D、4个4. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( )
A、70 B、75 C、80 D、853. 下列说法中:①同位角相等;②点到直线的距离是指这点到直线的垂线段;③在同一平面内,若有一条直线a和一点A , 则过点A可以作两条直线AC和AB垂直于直线a;④过直线外一点有且只有一条直线与已知直线平行;⑤平移前后的两个图形的对应点连线一定平行.以上命题中真命题的个数是( )A、1个 B、2个 C、3个 D、4个4. 如图,在中, , 将绕点逆时针旋转角度()得到 , 若 , 则的值为( ) A、 B、 C、 D、5. 如图,直线 , 点在上, , 垂足为若 , 则的度数为( )
A、 B、 C、 D、5. 如图,直线 , 点在上, , 垂足为若 , 则的度数为( ) A、 B、 C、 D、6. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )
A、 B、 C、 D、6. 如图, , , , , 给出以下结论: ; ; ; . 其中正确的结论有( )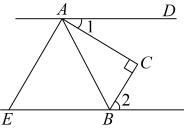 A、1个 B、2个 C、3个 D、4个7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )
A、1个 B、2个 C、3个 D、4个7. 如图,已知直线AB,CD被直线AC所截, , E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β,下列各式:①β﹣α,②α﹣β,③180°﹣α+β,④360°﹣α﹣β,可以表示∠AEC的度数的有( )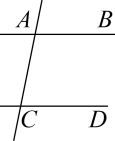 A、③④ B、①③④ C、①②④ D、②③④8. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.
A、③④ B、①③④ C、①②④ D、②③④8. 如图,已知 , , 点是射线上一动点(与点不重合),、分别平分和 , 分别交射线于点、 , 下列结论:①;②;③当时,;④当点运动时,的数量关系不变.其中正确结论有( )个.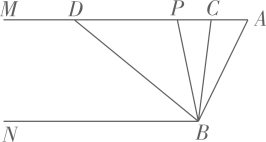 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,AB//CD,BC//ED,∠B=80°,则∠D=.
 10. 如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点, , 延长交于点 , 如果 , 那么的度数是 .
10. 如图,含有角的直角三角板的两个顶点放在一个长方形的对边上,点为直角顶点, , 延长交于点 , 如果 , 那么的度数是 . 11. 如图,AB∥EF, , , 已知∠FCD=60°,则∠P的度数为 .
11. 如图,AB∥EF, , , 已知∠FCD=60°,则∠P的度数为 . 12. 两块不同的三角板按如图所示摆放,边重合, , 接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间秒时,三角板有一条边与三角板的一条边恰好平行.
12. 两块不同的三角板按如图所示摆放,边重合, , 接着如图保持三角板不动,将三角板绕着点按顺时针以每秒的速度旋转后停止在此旋转过程中,当旋转时间秒时,三角板有一条边与三角板的一条边恰好平行. 13. 如图, , E为上一点,且垂足为F, , 平分 , 且 , 则下列结论:①;②平分;③;④;其中正确的有 . (请填写序号)
13. 如图, , E为上一点,且垂足为F, , 平分 , 且 , 则下列结论:①;②平分;③;④;其中正确的有 . (请填写序号)
三、解答题
-
14. 如图,已知AD⊥BC, FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
 15. 探究三角形的内角和(1)、下面是证明三角形内角和定理的一种添加辅助线的方法,请完成证明.
15. 探究三角形的内角和(1)、下面是证明三角形内角和定理的一种添加辅助线的方法,请完成证明.三角形的内角和定理:三角形的内角和等于180°.

已知:如图,△ABC
求证:∠A+∠B+∠C=180°
证明:在BC上任取一点D,过点D作DE∥AB,交AC于点E,过点D作DF∥AC,交AB于点F.
(2)、请再用一种不同的方法证明三角形内角和定理.四、综合题
-
16.

 (1)、已知AB∥CD,点M为平面内一点.如图①,BM⊥CM,小颖说过点M作MP∥AB,很容易说明∠ABM和∠DCM互余.请你帮小颖写出具体的证明过程.(2)、如图②,AB∥CD,点M在射线ED上运动,当点M移动到点A与点D之间时,试判断∠BMC与∠ABM,∠DCM的数量关系,并说明理由.(3)、在(2)的条件下,当点M在射线ED上的其他地方运动时(点M与E,A,D三点不重合),请直接写出∠BMC与∠ABM,∠DCM之间的数量关系.17. 如图1,线段是由线段平移得到的.分别连接 , . 直线于点 , 延长与相交于点 . 点是射线上的一个动点,点不与点、点、点重合.连接 , .
(1)、已知AB∥CD,点M为平面内一点.如图①,BM⊥CM,小颖说过点M作MP∥AB,很容易说明∠ABM和∠DCM互余.请你帮小颖写出具体的证明过程.(2)、如图②,AB∥CD,点M在射线ED上运动,当点M移动到点A与点D之间时,试判断∠BMC与∠ABM,∠DCM的数量关系,并说明理由.(3)、在(2)的条件下,当点M在射线ED上的其他地方运动时(点M与E,A,D三点不重合),请直接写出∠BMC与∠ABM,∠DCM之间的数量关系.17. 如图1,线段是由线段平移得到的.分别连接 , . 直线于点 , 延长与相交于点 . 点是射线上的一个动点,点不与点、点、点重合.连接 , .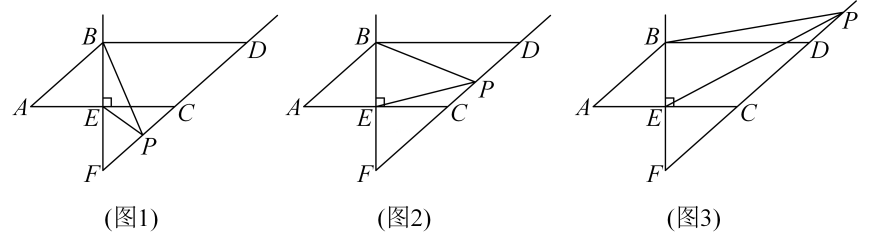 (1)、线段 , 的关系是;(2)、如图1,当点在线段上运动时, , , 之间的数量关系是;(3)、如图2,当点在线段上运动时, , , 之间的数量关系是否发生变化?若发生变化请写出它们的关系,并证明;若没有发生变化,请说明理由;(4)、如图3,当点在点上方运动时,请直接写出 , , 之间的数量关系: .
(1)、线段 , 的关系是;(2)、如图1,当点在线段上运动时, , , 之间的数量关系是;(3)、如图2,当点在线段上运动时, , , 之间的数量关系是否发生变化?若发生变化请写出它们的关系,并证明;若没有发生变化,请说明理由;(4)、如图3,当点在点上方运动时,请直接写出 , , 之间的数量关系: .