2023-2024学年冀教版初中数学七年级下册 7.2 相交线同步分层训练培优题
试卷更新日期：2024-01-27 类型：同步测试
一、选择题
-
1. 同一平面内互不重合的3条直线的交点的个数是（ ）A、可能是0，1，2 B、可能是0，2，3 C、可能是0，1，2或3 D、可能是1，可能是32. 如图，与∠α构成同位角的角的个数为（ ）
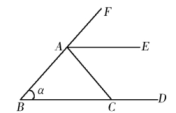A、1 B、2 C、3 D、43. 如图，直线AB，CD相交于点E，EF⊥AB于点E，若∠FEC-∠AEC=20°，那么∠AED的度数为（ ）
A、125° B、135° C、140° D、145°4. 小明在做一道数学题．直线AB，CD相交于点O，∠BOC＝25°，过点O作 ，求∠AOE的度数．小明得到 ，但老师说他少了一个答案．那么∠AOE的另一个值是（ ）A、105° B、115° C、125° D、135°5. 如图，取两根木条a，b，将它们钉在一起，得到一个相交线的模型．转动木条，当∠1增大10°时，有以下两种说法：①∠2增大10°；②∠3减小10．下列说法正确的是（ ）
A、①对，②不对 B、①不对，②对 C、①，②均不对 D、①，②均对6. 平面内两两相交的7条直线，其交点个数最少是m个，最多是n个，则m+n的值为（ ）A、18 B、20 C、22 D、247. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，那么六条直线最多有 （ ）A、21个交点 B、18个交点 C、15个交点 D、10个交点8. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（ ）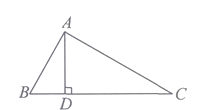
①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
⑥AD+BD>AB．
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 直线AB与直线CD相交于点 ， ， 射线 ， 则的度数为.10. 如图，同位角有a对，内错角有b对，同旁内角有c对，则a+b+c的值是 ．
11. 为了测量一座古塔外墙底部的底角∠AOB的度数，李潇同学设计了如下测量方案：分别作AO，BO的延长线OD，OC，量出∠COD的度数，从而得到∠AOB的度数．这个测量方案的依据是
12. 如图，在平面内，两条直线l1 ， l2相交于点O，对于平面内任意一点M，若p，q分别是点M到直线l1 ， l2 ， 的距离，则称（p，q）为点M的“距离坐标”．根据上述规定，“距离坐标”是（3，2）的点共有个．
13. 如图，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周，在旋转的过程中，当第秒时，直线CD恰好与直线MN垂直．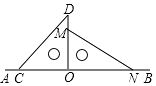
三、解答题
-
14. 如图，BCD是一条直线，∠1=∠B，∠2=∠A，指出∠1的同位角，∠2的内错角，并求出∠A+∠B+∠ACB的度数．
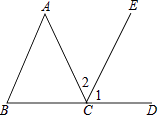15. 如图，已知A，O，E三点在一条直线上，OB平分∠AOC，∠AOB＋∠DOE＝90°，试问：∠COD与∠DOE之间有怎样的关系?说明理由.－com
四、综合题
-
16. 已知：直线AB与直线CD交于点O，过点O作 ．
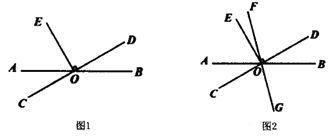(1)、如图1，若 ，求 的度数；(2)、如图2，过点O画直线FG满足射线OF在 内部，且使 ，在不添加任何辅助线的情况下，请直接写出与 互余的角．17. 已知，如图，点 、 分别代表两个村庄，直线 代表两个村庄之间的一条燃气管道，根据村民燃气需求，计划在管道 上某处修建一座燃气管理站，向两村庄接入管道．
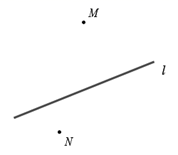(1)、若计划建一个离村庄 最近的燃气管理站，请画出燃气管理站的位置（用点 表示），并写出这样做的依据．(2)、若考虑到管道铺设费用问题，希望燃气管理站的位置到村庄 、村庄 距离之和最小，画出燃气管理站的位置（用点 表示），并写出这样做的依据．