2023-2024学年冀教版初中数学七年级下册 6.3 二元一次方程组的应用同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 《孙子算经》中有一道题,原文是:今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?小伟同学准备用二元一次方程组解决这个问题,他已列出一个方程是 , 则符合题意的另一个方程是( )A、 B、 C、 D、2. 现用190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,若做成的盒身与盒底恰好完全配套,设用x张铁皮做盒身,y张铁皮做盒底,则可列方程组为( )A、 B、 C、 D、3. 母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将20元钱全部用于购买这两种花(两种花都买) ,小明的购买方案共有 ( )A、2种 B、3种 C、4种 D、5种4. 九章算术中记载了一个问题,大意是:有几个人一起去买一件物品,每人出元,多元;每人出元,少元问有多少人?小红是这样想的:设有人,物品价值元,她先列了一个方程 , 请你帮她再列出另一个方程( )A、 B、 C、 D、5. 为鼓励学生积极参加阳光体育健身活动,某学校计划购买一批篮球和足球若购买个篮球,个足球,需花费元;若购买个篮球,个足球,需花费元则篮球、足球的单价各是多少元?设篮球的单价为元,足球的单价为元,则下列方程组正确的是( )A、 B、
C、 D、6. 有两个正方形 , ,将 , 并列放置后构造新的长方形得到图甲,将 , 并列放置后构造新的正方形得到图乙,若图甲和图乙中阴影部分的面积分别为10和32,则正方形 的面积为( )
 A、4 B、5 C、6 D、77. 爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下
A、4 B、5 C、6 D、77. 爸爸开车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下时刻
9:00
9:45
12:00
碑上的数
是一个两位数,数字之和是9
十位与个位数字与9:00时所看到的正好相反
比9:00时看到的两位数中间多了个0
9:00时看到的两位数是( )
A、54 B、45 C、36 D、278. “幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现将填入如图2所示的“幻方”中,部分数据已填入,则的值为( )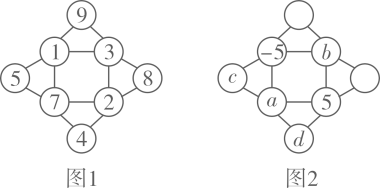 A、-50 B、 C、50 D、
A、-50 B、 C、50 D、二、填空题
-
9. 某眼镜厂有工人25名,每人每天平均生产镜架9个或镜片12片.为了使每天生产的镜架和镜片刚好配套,设x名工人生产镜架,y名工人生产镜片,则可列出方程组:.10. 如图,射线OC的端点O在直线AB上,已∠1比∠2的2倍多10°,设∠1=x°,∠2=y°,则列出关于x,y的方程组是:.
 11. “幻方”最早记载于春秋时期的《大戴礼》中,现将这8个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是 .
11. “幻方”最早记载于春秋时期的《大戴礼》中,现将这8个数字填入如图1所示的“幻方”中,使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图2所示的“幻方”,则的值是 . 12. 某食品加工厂在端午节期间制作红枣粽、腊肉粽、咸蛋粽进行销售,去年端午节期间销售的这三种粽子的数量之比为2∶3∶1,今年端午节期间销售这三种粽子不光保持了去年的销量,而且都还有所增加,其中腊肉粽增加的销量占今年总增加销量的 . 今年腊肉粽销售的数量占三种粽子销售总数量的 , 而红枣粽销售的总数量是咸蛋粽销售的总数量的2倍,则去年咸蛋粽销售的数量与今年咸蛋粽销售的数量之比为 .13. 为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种粗粮每袋装有3千克粗粮,1千克粗粮,1千克粗粮;乙种粗粮每袋装有1千克粗粮,2千克粗粮,2千克粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的 , , 三种粗粮的成本价之和.已知粗粮每千克成本价为元,甲种粗粮每袋售价为58.5元,利润率为30%,乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%,则该电商销售甲、乙两种袋装粗粮的数量之比是.(商品的利润率)
12. 某食品加工厂在端午节期间制作红枣粽、腊肉粽、咸蛋粽进行销售,去年端午节期间销售的这三种粽子的数量之比为2∶3∶1,今年端午节期间销售这三种粽子不光保持了去年的销量,而且都还有所增加,其中腊肉粽增加的销量占今年总增加销量的 . 今年腊肉粽销售的数量占三种粽子销售总数量的 , 而红枣粽销售的总数量是咸蛋粽销售的总数量的2倍,则去年咸蛋粽销售的数量与今年咸蛋粽销售的数量之比为 .13. 为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种粗粮每袋装有3千克粗粮,1千克粗粮,1千克粗粮;乙种粗粮每袋装有1千克粗粮,2千克粗粮,2千克粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的 , , 三种粗粮的成本价之和.已知粗粮每千克成本价为元,甲种粗粮每袋售价为58.5元,利润率为30%,乙种粗粮的利润率为20%若这两种袋装粗粮的销售利润率达到24%,则该电商销售甲、乙两种袋装粗粮的数量之比是.(商品的利润率)三、解答题
-
14. 要用20张白卡纸做包装盒,每张白卡纸可以做盒身2个或做底盖3个.如果1个盒身和2个底盖可以做成一个包装盒,那么能否把这些白卡纸分成两部分,一部分做盒身,一部分做底盖,使做成的盒身和底盖正好配套?请你设计一种方法:如果不允许剪开白卡纸,能不能找到符合题意的方法?如果允许剪开一张白卡纸,怎样才能既符合题意又能最充分地利用白卡纸?15. 当下公园露营正成为人们一种新的周末休闲娱乐方式.某户外用品店老板决定采购一批帐篷进行销售,已知A型普通帐篷的进价比B型简易帐篷多100元,购买40顶A型帐篷和60顶B型帐篷的金额相同.(1)、每顶A型帐篷和B型帐篷的进价分别是多少元?(2)、8月份该店以a元每顶售出A型帐篷120顶,以b元每顶售出B型帐篷150顶.销售收入合计为79200元.
①用含a的式子来表示b;
②9月份该店根据市场变化决定每顶A型帐篷的售价不变,每顶B型帐篷的售价在8月的基础上下降了元,9月份A型帐篷的销售数量比8月份增加了60顶,B型帐篷的销售数量是8月份的 , 该店9月份销售这两种帐篷共获利12600元,求a的值.
四、综合题
-
16. 5月至10月,广东省居民阶梯电价实行“夏季模式”,具体收费标准如下表:
档次
用电量(度)
单价(元/度)
第一档
不超过260
x
第二档
超过260,不超过600的部分
y
第三档
超过600的部分
0.9
小海家2021年7月、8月用电量分别是560度和760度,缴纳电费分别为351元和521元.
(1)、求表中的x和y的值;(2)、广东省自2021年6月1日起执行居民阶梯电价“一户多人口”政策,如果一户家庭人口满5人及以上可申请每户每月第一、二、三档分别增加100度阶梯电量基数.小海家庭人口为6人,若申请“一户多人口”政策,小海家2021年7、8月份共可省多少电费?17. 某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是230cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图所示,(单位:cm) (1)、写出图甲中m与n的值,m= , n= .(2)、在试生产阶段,若将a张标准板材用裁法一裁剪,b张标准板材用载法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式(长大于宽)无盖礼品盒.
(1)、写出图甲中m与n的值,m= , n= .(2)、在试生产阶段,若将a张标准板材用裁法一裁剪,b张标准板材用载法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙横式(长大于宽)无盖礼品盒.①两种裁法共产生A型板材 张,B型板材 张(用含有a、b的代数式表示)
②当10<b<20时,所截得的A型板材和B型板材恰好配套用完,做成的横式无盖礼品盒可能是 个.(在横线上直接写出所有可能答案,无需书写过程)