2023-2024学年湘教版初中数学九年级下册 2.7 正多边形与圆同步分层训练基础题
试卷更新日期：2024-01-27 类型：同步测试
一、选择题
-
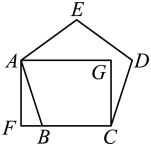
1. 如图，正方形ABCD内接于⊙O，点P在 上，则∠BPC的度数为（ ）
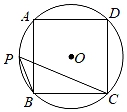A、30° B、45° C、60° D、90°2. 将一个正六边形绕其中心旋转后仍与原图形重合，旋转角的大小不可能是（ ）A、60° B、90° C、180° D、360°3. 如图，正五边形ABCDE内接于⊙O ， 连结OC ， OD ， 则∠COD＝（ ）
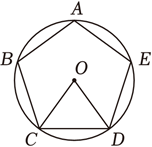A、72° B、60 C、54 D、48°4. 若正边形的一个外角为 ， 则的值是（ ）A、6 B、5 C、4 D、35. 一个圆的内接正六边形与内接正方形的边长之比为（ ）A、3：2 B、 C、 D、6. 已知一个三角形的内心与外心重合，若它的内切圆的半径为2，则它的外接圆的面积为（ ）A、 B、 C、 D、7. 如图，正六边形内接于 ， 的半径为6，则这个正六边形的边心距和的长分别为（ ）
A、3， B、 ， C、 ， D、 ，8. 作⊙O的内接正六边形ABCDEF ， 甲、乙两人的作法分别是：甲：第一步：在⊙O上任取一点A ， 从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B ， C ， D ， E ， F ． 第二步：依次连接这六个点．
乙：第一步：任作一直径AD ． 第二步：分别作OA ， OD的中垂线与⊙O相交，交点从点A开始，依次为点B ， C ， E ， F ． 第三步：依次连接这六个点．
对于甲、乙两人的作法，可判断（ ）
A、甲正确，乙错误 B、甲、乙均错误 C、甲错误，乙正确 D、甲、乙均正确二、填空题
-
9. 如图所示的图案绕中心旋转n°后能与原来的图案完全重合，则n的最小值为
10. 如图，△ABC是边长为a的等边三角形纸张，现将各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则此正六边形的周长等于
11. 用“筝形”和“镖形”两种不同的瓷砖铺设成如图所示的地面，则“筝形”瓷砖中的内角 °.
12. 将三个相同的六角形螺母并排摆放在桌面上，从上面看到的图形如图1所示，正六边形边长为3且各有一个顶点在直线l上，则图1中螺母组成的图形的周长（图中加粗部分总长度）为；两侧螺母不动，把中间螺母抽出并重新摆放后，从上面看到的图形如图11-2所示，其中，中间正六边形的一边与直线l平行，有两边分别经过两侧正六边形的一个顶点，正六边形边直线l ． 则 ．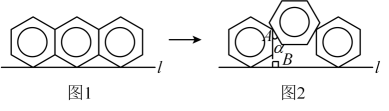
13. 我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术：“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．“割圆术”孕育了微积分思想，他用这种思想得到了圆周率的近似值为3.1416．如图，的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计的面积，可得的估计值为 ， 若用圆内接正十二边形作近似估计，可得的估计值为 ．
三、解答题
-
14. 已知：如图，在圆内接正五边形ABCDE中，对角线AC，BD交于点P．
(1)、求∠APD的度数．(2)、求证：四边形EAPD是菱形．15. 如图，正六边形ABCDEF内接于.
(1)、若P是上的动点，连接BP ， FP ， 求的度数；(2)、已知的面积为.①求的度数；
②求的半径.
四、综合题
