2023-2024学年湘教版初中数学九年级下册 2.6 弧长与扇形面积同步分层训练基础题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为（）

A、 $\frac{3}{2} π$ B、 $2 π$ C、 $3 π$ D、 $6 π$

查看试题解析
2. 已知一个扇形的圆心角为150°，半径是6，则这个扇形的面积是（　　）

A、15π B、10π C、5π D、2.5π

查看试题解析
3. 已知在半径为R的圆中，长为l的弧所对的圆心角度数为n°，则下列关系不正确的是（）

A、l= $\frac{π n R}{180}$ B、n= $\frac{180 l}{π R}$ C、R= $\frac{180 l}{π n}$ D、l=2nR

查看试题解析
4. 如图，点A，B，C是⊙O上的点，且∠ACB=40°，阴影部分的面积为2π，则此扇形的半径为（）．

A、2 B、3 C、4 D、5

查看试题解析
5. 如图，在△ABC中，∠ABC=90°，∠ACB=30°，AB=4，点O为BC的中点，以O为圆心，OB长为半径作半圆，交AC于点D，则图中阴影部分的面积是（）

A、 $5 \sqrt{3} - \frac{\sqrt{3}}{3} π$ B、 $5 \sqrt{3} - 4 π$ C、 $5 \sqrt{3} - 2 π$ D、 $10 \sqrt{3} - 2 π$

查看试题解析
6. 台州S₁轻轨在紧张施工中，现在已开始隧道挖掘作业，如图1，圆弧形混凝土管片是构成圆形隧道的重要部件，如图2，有一圆弧形混凝土管片放置在水平地面上，底部用两个完全相同的长方体木块固定，为估计隧洞开挖面的大小，甲、乙两个小组对相关数据进行测量方案如表，利用数据能够估算隧道外径大小的小组是（　　）
小组
测量内容
甲
HG ， GN的长
乙
AB ， $\hat{A D} ， \hat{B C}$ 的长

A、甲小组 B、乙小组 C、两组都可以 D、两组测量数据都不足

查看试题解析
7. 如图，在Rt△ABC中，∠C＝90°，∠A＝60°，BC＝ $\sqrt{3}$ ，将△ABC绕点B旋转到△A₁BC₁的位置，此时C ， B ， A₁在同一直线上，则点A经过的最短路径长为（　　）

A、 $\frac{5 π}{6}$ B、 $\frac{5 \sqrt{3} π}{6}$ C、 $\frac{5 \sqrt{3} π}{3}$ D、 $\frac{5 π}{3}$

查看试题解析
8. 如图， $⊙ O$ 中，弦 $A B ⊥ C D$ 于 $E$ ，若 $∠ A = 30 ° ， ⊙ O$ 的半径等于6，则弧 $A C$ 的长为（）

A、 $6 π$ B、 $5 π$ C、 $4 π$ D、 $3 π$

查看试题解析

二、填空题

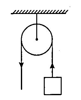
9. 已知一扇形，半径为6，圆心角为120°，则所对的弧长为.

查看试题解析
10. 如图，用一个半径为6 cm的定滑轮拉动重物上升，滑轮旋转了120°，假设绳索粗细不计，且与轮滑之间没有滑动，则重物上升了cm（结果保留式）.

查看试题解析
11. 如图，在半径为2的扇形 $O A B$ 中， $∠ A O B = 90 °$ ，将扇形 $O A B$ 沿过点B的直线折叠，点O恰好落在弧 $A B$ 上，折痕交 $O A$ 于点C ，则图中阴影部分的周长是.

查看试题解析
12. 扇形的圆心角为80°，弧长为4πcm，则此扇形的面积等于cm² ．

查看试题解析
13. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D＝110°，则 $\overset{⌢}{A C}$ 的长为.

查看试题解析

三、解答题

14. 如图， $A$ ， $B$ 是 $⊙ O$ 上的点， $P$ 为 $⊙ O$ 外一点，连结 $P A$ ， $P B$ ，分别交 $⊙ O$ 于点 $C$ ， $D$ ，且 $\overset{⌢}{A C} = \overset{⌢}{B D}$ ．

(1)、求证： $P A = P B$ ；

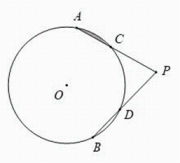(2)、若 $⊙ O$ 的半径为6， $∠ P = 60 °$ ， $\overset{⌢}{C D} = 3 \overset{⌢}{A C}$ ，求图中阴影部分的面积．

查看试题解析
15. 如图，正方形网格中有一段弧，弧上三点A ， B ， C均在格点上．

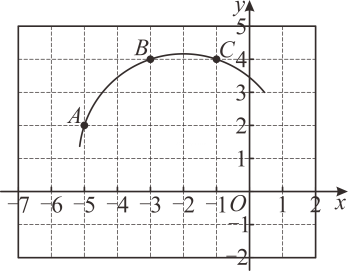(1)、请作图找出圆心P的位置，并写出它的坐标．

(2)、求 $\overset{⏜}{A C}$ 的长度．

查看试题解析

四、综合题

16. 如图，网格中每个小正方形的边长均为1个单位长度，△ABC的三个顶点都在网格的格点上.

(1)、将△ABC绕点B顺时针旋转90°得到△A'BC'，请在网格中画出△A'BC'；

(2)、在（1）的条件下，求出点A经过的路程（结果保留π）.

查看试题解析
17. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $B D$ 是 $⊙ O$ 的直径， $A B = A C ， A E ∥ B C$ ， E为 $B D$ 的延长线与 $A E$ 的交点．

(1)、求证： $A E$ 是 $⊙ O$ 的切线；

(2)、若 $∠ A B C = 75 ° ， B C = 2$ ，求 $\overset{⌢}{C D}$ 的长．

查看试题解析

小组	测量内容
甲	HG ， GN的长
乙	AB ， $\hat{A D} ， \hat{B C}$ 的长