2023-2024学年湘教版初中数学九年级下册 2.5 直线与圆的位置关系同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1.
如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2 , 那么∠AOB等于( )
 A、90° B、100° C、110° D、120°2. 《数书九章》是我国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边a,b,c求面积的公式.若三角形的三边a,b,c分别为7,6,3,则这个三角形内切圆的半径是( )A、 B、 C、 D、3. 如图,在中,是边上的点,以为圆心,为半径的与相切于点 , 平分 , , , 的长是( )
A、90° B、100° C、110° D、120°2. 《数书九章》是我国南宋时期杰出数学家秦九韶的著作,书中提出了已知三角形三边a,b,c求面积的公式.若三角形的三边a,b,c分别为7,6,3,则这个三角形内切圆的半径是( )A、 B、 C、 D、3. 如图,在中,是边上的点,以为圆心,为半径的与相切于点 , 平分 , , , 的长是( ) A、 B、2 C、 D、4. 如图,在平面直角坐标系中,点P 在第一象限,⊙P与x轴相切于点Q,与y轴交于 , 两点,则点P的坐标是 ( )
A、 B、2 C、 D、4. 如图,在平面直角坐标系中,点P 在第一象限,⊙P与x轴相切于点Q,与y轴交于 , 两点,则点P的坐标是 ( )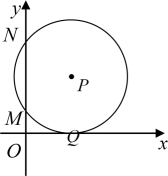 A、(5,3) B、(3,5) C、(4,5) D、(5,4)5. 如图, 中, , ,它的周长为 若 与 , , 三边分别切于 , , 点,则 的长为( )
A、(5,3) B、(3,5) C、(4,5) D、(5,4)5. 如图, 中, , ,它的周长为 若 与 , , 三边分别切于 , , 点,则 的长为( )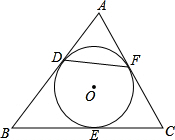 A、2 B、3 C、4 D、56. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( )
A、2 B、3 C、4 D、56. 如图,不等边内接于 , I是其内心, , , , 内切圆半径为( ) A、4 B、 C、 D、7. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
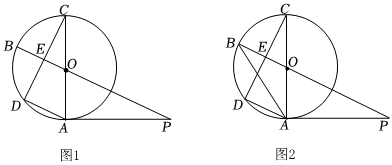
A、4 B、 C、 D、7. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )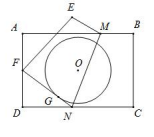 A、3.6 B、 C、3.5 D、8. 如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A、3.6 B、 C、3.5 D、8. 如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )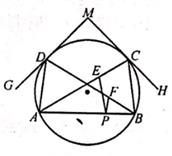 A、4 B、2 C、4 D、值不确定
A、4 B、2 C、4 D、值不确定二、填空题
-
9. 如图,在中, , . , 与延长线、、延长线相切,切点分别为、、 , 则点到圆心的距离为.
 10. 如图,中, , 为的角平分线,以点O为圆心,为半径作与边交于点D.若 , , 则.
10. 如图,中, , 为的角平分线,以点O为圆心,为半径作与边交于点D.若 , , 则. 11. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为.
11. 我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为. 12. 一个边长为3cm的正它有一个外接圆⊙O,我们记为第1个圆,它的内切圆记为第2个圆;在第2个圆内作一个内接正△的内切圆,记为第3个圆;在第3个圆内作一个内接正△的内切圆,记为第4个圆,…,如此作下去,那么第2022个圆的半径是cm
12. 一个边长为3cm的正它有一个外接圆⊙O,我们记为第1个圆,它的内切圆记为第2个圆;在第2个圆内作一个内接正△的内切圆,记为第3个圆;在第3个圆内作一个内接正△的内切圆,记为第4个圆,…,如此作下去,那么第2022个圆的半径是cm 13. 如图 1, 是某激光黑白 A4 纸张打印机的机身,其侧面示意图如图 2,AB⊥BC,CD⊥BC.出纸盘 EP 下方为一段以 O 为圆心的圆弧 , 与上部面板线段 AE 交于点 E,与 CD 相切于点 D.测得 BC=24cm, CD=18cm.进纸盘 CH 可以随调节扣 HF 向右平移,CH=18cm,HF=2cm.当 HF 向右移动 6cm 至H′F′时,点 A,D,F'在同一直线上,则 AB 的长度为cm.若点 E 到 AB 的距离为 16cm, tanA=4,连接 PO,线段 OP 恰好过圆弧的中点.若点 P 到直线 BC 的距离为 32cm,则 PE=cm.
13. 如图 1, 是某激光黑白 A4 纸张打印机的机身,其侧面示意图如图 2,AB⊥BC,CD⊥BC.出纸盘 EP 下方为一段以 O 为圆心的圆弧 , 与上部面板线段 AE 交于点 E,与 CD 相切于点 D.测得 BC=24cm, CD=18cm.进纸盘 CH 可以随调节扣 HF 向右平移,CH=18cm,HF=2cm.当 HF 向右移动 6cm 至H′F′时,点 A,D,F'在同一直线上,则 AB 的长度为cm.若点 E 到 AB 的距离为 16cm, tanA=4,连接 PO,线段 OP 恰好过圆弧的中点.若点 P 到直线 BC 的距离为 32cm,则 PE=cm.


三、解答题
-
14.
如图,AB是⊙O的直径,点F、C在⊙O上且
 , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线;
(2)若
 , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径. 15. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
15. 平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).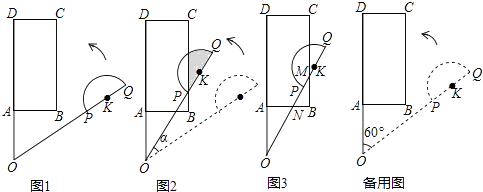
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
四、综合题