湘教版数学九年级下册 2.4 过不共线三点作圆同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 已知在Rt△ABC中,∠C=90°,AC=5,BC=12,则△ABC的外接圆直径为( )A、5 B、12 C、13 D、6.52. 在平面直角坐标系中,已知点A(0,1),B(0,﹣5),若在x轴正半轴上有一点C,使∠ACB=30°,则点C的横坐标是( )A、3 4 B、12 C、6+3 D、63. 如图,在平面直角坐标系中,点A、B、C的坐标为、、 , 则外接圆的圆心坐标是( )
 A、 B、 C、 D、4. 已知锐角中,O是的中点,甲、乙二人想在上找一点P , 使得的外心为点O , 其做法如图.对于甲、乙二人的做法,正确的是( )
A、 B、 C、 D、4. 已知锐角中,O是的中点,甲、乙二人想在上找一点P , 使得的外心为点O , 其做法如图.对于甲、乙二人的做法,正确的是( ) A、两人都正确. B、只有甲正确 C、只有乙正确 D、两人都不正确5. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )
A、两人都正确. B、只有甲正确 C、只有乙正确 D、两人都不正确5. 如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )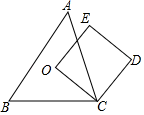 A、O是△AEB的外心,O不是△AED的外心 B、O是△BEC的外心,O不是△BCD的外心 C、O是△AEC的外心,O不是△BCD的外心 D、O是△ADB的外心,O不是△ADC的外心6. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A、O是△AEB的外心,O不是△AED的外心 B、O是△BEC的外心,O不是△BCD的外心 C、O是△AEC的外心,O不是△BCD的外心 D、O是△ADB的外心,O不是△ADC的外心6. 如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( ) A、 B、 C、 D、7. 如图,在中, , 分别作 , 两边的垂直平分线、 , 垂足分别是点M、N,以下说法:①;②;③;④点P到点B和点C的距离相等.其中正确的是( )
A、 B、 C、 D、7. 如图,在中, , 分别作 , 两边的垂直平分线、 , 垂足分别是点M、N,以下说法:①;②;③;④点P到点B和点C的距离相等.其中正确的是( )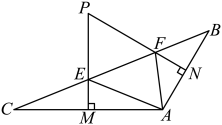 A、①②③ B、①②④ C、①③④ D、②③④8. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )
A、①②③ B、①②④ C、①③④ D、②③④8. 如图,直线l:分别与x轴、y轴交于点A、B . 点P为直线l在第一象限的点.作△POB的外接圆 , 延长OC交于点D , 当△POD的面积最小时,则的半径长为( )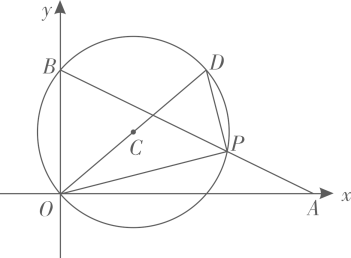 A、 B、2 C、 D、3
A、 B、2 C、 D、3二、填空题
-
9. 在中, , 则的外接圆的半径为 .10. 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= , 则BD的长为
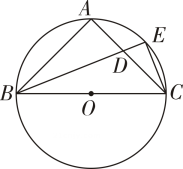 11. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是
11. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.用一个圆面去覆盖△ABC,能够完全覆盖这个三角形的最小圆面的半径是 12. 如图,已知半圆O , OB= . 点D在半圆上,AD=10,在取点C , 连结AC , 作DH⊥AC于点H , 连结BH , 则BH的最小值等于 .
12. 如图,已知半圆O , OB= . 点D在半圆上,AD=10,在取点C , 连结AC , 作DH⊥AC于点H , 连结BH , 则BH的最小值等于 . 13. 如图,在等腰三角形纸片中, , 将该纸片翻折,使得点C落在边的F处,折痕为 , D,E分别在边 , 上, , 若 , , 则 , 的面积为.
13. 如图,在等腰三角形纸片中, , 将该纸片翻折,使得点C落在边的F处,折痕为 , D,E分别在边 , 上, , 若 , , 则 , 的面积为.
三、解答题
-
14. 如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.若抛物线的顶点D的坐标为(1,4).
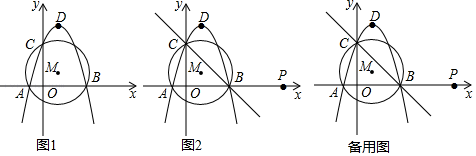 (1)、求抛物线的解析式,及A、B、C三点的坐标;(2)、求⊙M的半径和圆心M的坐标;(3)、如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.15. 如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
(1)、求抛物线的解析式,及A、B、C三点的坐标;(2)、求⊙M的半径和圆心M的坐标;(3)、如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.15. 如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD= , 求⊙O的半径.

四、综合题
-
16. 已知菱形ABCD的边长为4.∠ADC=60°,等边△AEF两边分别交边DC,CB于点E,F.
 (1)、特殊发现:如图1,若点E,F分别是边DC,CB的中点.求证:菱形ABCD对角线AC,BD的交点O即为等边△AEF的外心;(2)、若点E,F始终分别在边DC,CB上移动,等边△AEF的外心为点P.
(1)、特殊发现:如图1,若点E,F分别是边DC,CB的中点.求证:菱形ABCD对角线AC,BD的交点O即为等边△AEF的外心;(2)、若点E,F始终分别在边DC,CB上移动,等边△AEF的外心为点P.①猜想验证:如图2.猜想△AEF的外心P落在哪条直线上,并加以证明;
②学以致用:如图3,当△AEF的面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,求的值.
17. 综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
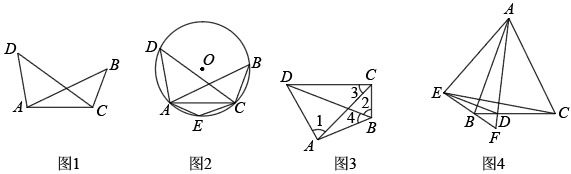
提出问题:
如图1,在线段AC同侧有两点B,D,连接 , 如果 , 那么A,B,C,D四点在同一个圆上.
探究展示:求证:点A,B,C,D四点在同一个圆上
如图2,作经过点A,C,D的 , 在劣弧上取一点E(不与A,C重合),连接 , , 则.
(1)、请完善探究展示(2)、如图3,在四边形中, , 则∠4的度数为.(3)、拓展探究:如图4,已知是等腰三角形, , 点D在上(不与的中点重合),连接.作点C关于的对称点E,连接并延长交的延长线于F,连接.①求证:A,D,B,E四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由