2023-2024学年湘教版初中数学九年级下册 2.3 垂径定理同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1.
如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为 $\sqrt{3} c m$ ，则弦CD的长为（）

A、 $\frac{3}{2} c m$ B、 $3 c m$ C、 $2 \sqrt{3} c m$ D、 $9 c m$

查看试题解析
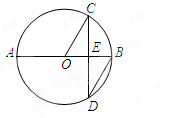2. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，且AB是 $⊙ O$ 的直径，点P为 $⊙ O$ 上的动点，且 $∠ B P C = 60 °$ ， $⊙ O$ 的半径为6，则点P到AC距离的最大值是（）

A、6 B、12 C、 $6 + 3 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
3. 下列语句，错误的是（）

A、直径是弦 B、过圆心的弦是直径 C、平分弧的直径垂直于弧所对的弦 D、相等的圆心角所对的弧相等

查看试题解析
4. 如图，在一个残缺的圆形工件上量得弦 $B C = 8 c m$ ， $\overset{⏜}{B C}$ 的中点 $D$ 到弦 $B C$ 的距离 $D E = 2 c m$ ，则这个圆形工件的半径是（）

A、 $4.5 c m$ B、 $5 c m$ C、 $5.5 c m$ D、 $6 c m$

查看试题解析
5. 如图，某大桥的桥拱可以近似地看作半径为250m的圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面 $A B$ 长度为300m，那么这些钢索中最长的一根为（）

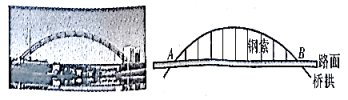A、40m B、45m C、50m D、60m

查看试题解析
6. 如图，CD为⊙O的直径，弦AB⊥CD于E，CE=1，AB=10，那么直径CD的长为（）

A、12.5 B、13 C、25 D、26

查看试题解析
7. 如图所示，在 $⊙ O$ 中，点C在优弧AB上，将弧BC沿BC折叠后，刚好经过AB的中点 $D$ .若 $⊙ O$ 的半径为 $2 \sqrt{5} ， A B = 8$ ，则BC的长是（）.

A、 $5 \sqrt{3}$ B、 $\frac{\sqrt{255}}{2}$ C、 $6 \sqrt{2}$ D、 $\frac{14 \sqrt{5}}{3}$

查看试题解析
8. 一次综合实践的主题为：只用一张矩形纸条和刻度尺，如何测量一次性纸杯杯口的直径？小聪同学所在的学习小组想到了如下方法：如图，将纸条拉直紧贴杯口上，纸条的上下边沿分别与杯口相交于A ， B ， C ， D四点，利用刻度尺量得该纸条宽为 $3.5 c m$ ， $A B = 3 c m$ ， $C D = 4 c m$ 。请你帮忙计算纸杯的直径为（）

A、 $4 c m$ B、 $5 c m$ C、 $6 c m$ D、 $7 c m$

查看试题解析

二、填空题

9. 如图是一个管道的横截面，管道的截面的半径为 $5 c m$ ，管道内水的最大深度 $C D = 2 c m$ ，则截面圆中弦 $A B$ 的长为 $c m$ ．

查看试题解析
10. 如图， $⊙ O$ 的半径 $O E ⊥ A C$ 于点D，连接AO并延长，交 $⊙ O$ 于点B ，连接BE．
⑴若 $∠ B = 27 °$ ，则 $∠ A$ 的度数为。
⑵若 $A C = 8$ ， $D E = 2$ ，则 $⊙ O$ 的半径长为。

查看试题解析
11. “圆”是中国文化的一个重要精神元素，在中式建筑中有着广泛的应用.例如古典园林中的门洞，如图，某地园林中的一个圆弧形门洞的高为2.5m，地面入口宽为1m，则该门洞的半径为 m.

查看试题解析
12. 如图，四边形ABCD内接于⊙O，AC是⊙O的直径，BD平分∠ABC．若AB=3，BC=4，则BD的长为.

查看试题解析
13. 图1是某游乐园的摩天轮，A，B两位同学坐在摩天轮上的示意图如图2，摩天轮半径OA为9米，两同学的直线距离AB为6米，当两位同学旋转到同一高度时（A在B的右侧），A同学距离地面的高度为米，当A同学旋转到最高位置，此时两位同学的高度差为米．

查看试题解析

三、解答题

14. 如图，△ABD内接于半圆O，AB是直径，点C是弧BD的中点，连结OC，AC，分别交BD于点F、E．

(1)、求证： $O C ∥ A D$ ；

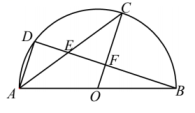(2)、若 $A B = 10 ， A C = 8$ ，求 $A D$ 的长．

查看试题解析
15. 如图，△ABC内接于⊙O，过点O作OH⊥BC于点H，延长OH交⊙O于点D，连接AD、BD，AD与BC交于点E，AD＝9．

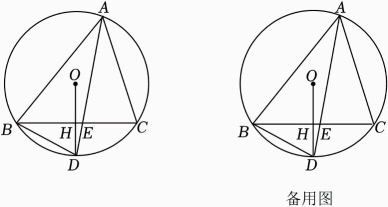(1)、求证：∠BAD＝∠CAD．

(2)、若OH＝DH．
①求∠BAC的度数．
②若⊙O的半径为6，求DE的长．

(3)、设BD＝x，AB⋅CE＝y，求y关于x的函数表达式．

查看试题解析

四、综合题

16. 如图， $M N$ 为 $⊙ O$ 的直径，且 $M N = 15$ ， $M C$ 与 $N D$ 为圆内的一组平行弦，弦 $A B$ 交 $M C$ 于点H.点A在 $\overset{⌢}{M C}$ 上，点B在 $\overset{⌢}{N C}$ 上， $∠ O N D + ∠ A H M = 90 °$ .

(1)、求证： $M H \cdot C H = A H \cdot B H$ .

(2)、求证： $\overset{⌢}{A C} = \overset{⌢}{B C}$ .

(3)、在 $⊙ O$ 中，沿弦 $N D$ 所在的直线作劣弧 $\overset{⌢}{N D}$ 的轴对称图形，使其交直径 $M N$ 于点G.若 $s i n ∠ C M N = \frac{3}{5}$ ，求 $N G$ 的长.

查看试题解析
17. 问题背景：如图1， $A B$ 是 $⊙ O$ 的直径，点 $C$ ，点 $D$ 在圆上（在直径 $A B$ 的异侧），且 $D$ 为弧 $A B$ 的中点，连接 $A D$ ， $B D$ ， $C D$ ， $A C$ ， $B C$ ．
探究思路：如图2，将 $△ A D C$ 绕点 $D$ 顺时针旋转 $90 °$ 得到 $△ B D E$ ，证明 $C$ ， $B$ ， $E$ 三点共线，从而得到 $△ D C E$ 为等腰直角三角形， $B C + B E = \sqrt{2} C D$ ，从而得出 $A C + B C = \sqrt{2} C D$ ．

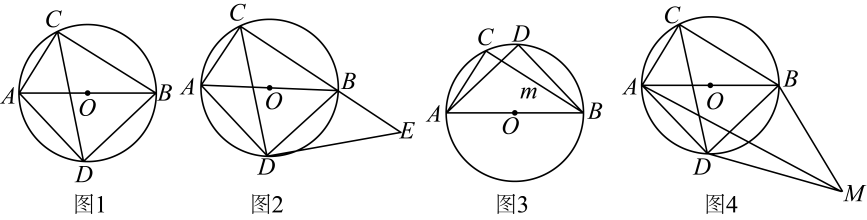(1)、请你根据探究思路，写出完整的推理过程；

(2)、问题解决：
若点 $C$ ，点 $D$ 在直径 $A B$ 的同侧，如图3所示，且点 $D$ 为弧 $A B$ 的中点，连接 $C D$ ， $B C = m$ ， $A C = n (m > n)$ ，直接写出线段 $C D$ 的长为（用含有 $m$ ， $n$ 的式子表示）；

(3)、拓展探究：
将 $△ C B D$ 沿 $B D$ 翻折得到 $△ M B D$ ，如图4所示，试探究： $M A$ ， $M B$ ， $M D$ 之间的数量关系，并说明理由．

查看试题解析