湘教版数学九年级下册 2.3 垂径定理同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
 A、8cm B、5cm C、3cm D、2cm2. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个3. 如图,线段是的直径,于点E , 若长为16,长为6,则半径是( )
A、8cm B、5cm C、3cm D、2cm2. 下列语句中:①平分弦的直径垂直于弦;②相等的圆心角所对的弧相等;③长度相等的两条弧是等弧;④圆是轴对称图形,任何一条直径都是它的对称轴;⑤在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等,不正确的有( )A、2个 B、3个 C、4个 D、5个3. 如图,线段是的直径,于点E , 若长为16,长为6,则半径是( )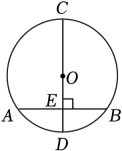 A、5 B、6 C、8 D、104. 如图,CD是⊙O的直径,AB是弦且不是直径,CD⊥AB,则下列结论不一定正确的是( )
A、5 B、6 C、8 D、104. 如图,CD是⊙O的直径,AB是弦且不是直径,CD⊥AB,则下列结论不一定正确的是( ) A、AE=BE B、OE=DE C、AO=CO D、5. 一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心O到水面的距离是( )
A、AE=BE B、OE=DE C、AO=CO D、5. 一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心O到水面的距离是( ) A、4 B、3 C、2 D、16. 如图,是的弦,点是上的动点(不与点 , 重合),过点作垂直于的弦 . 若设的半径为 , , , 则弦的长( )
A、4 B、3 C、2 D、16. 如图,是的弦,点是上的动点(不与点 , 重合),过点作垂直于的弦 . 若设的半径为 , , , 则弦的长( ) A、与 , , 的值均有关 B、只与 , 的值有关 C、只与的值有关 D、只与 , (或 , )的值有关7. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或8. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )
A、与 , , 的值均有关 B、只与 , 的值有关 C、只与的值有关 D、只与 , (或 , )的值有关7. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或8. 如图,中,点C为弦中点,连接 , , , 点D是上任意一点,则度数为( )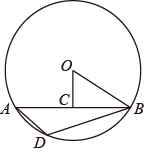 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,我国古代建造的闻名中外的赵州石拱桥,若桥拱圆弧的半径长为 , 拱高为 , 则桥跨度为(用含r、h的代数式表示)
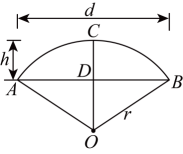 10. 如图3-3所示为一条直径为2m的通水管道的轴截面,其水面宽1.6m,则这条管道中水最深为m.
10. 如图3-3所示为一条直径为2m的通水管道的轴截面,其水面宽1.6m,则这条管道中水最深为m. 11. 往直径为的圆柱形容器内装入一些水以后,截面如图所示,且圆心在水面上方.若水面宽 , 则水的最大深度为 .
11. 往直径为的圆柱形容器内装入一些水以后,截面如图所示,且圆心在水面上方.若水面宽 , 则水的最大深度为 .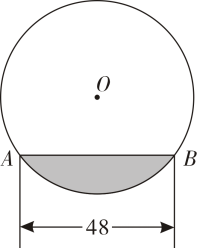 12. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
12. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为 .
13. 如图,在边长为1的正方形网格中,⊙O是△ABC的外接圆,点A,B,O在格点上,则cos∠ACB的值是 .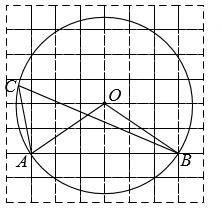
三、解答题
-
14. 石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为 . 桥的跨度(弧所对的弦长)AB=24m,设所在圆的圆心为O,半径OC⊥AB,垂足为D.拱高(弧的中点到弦的距离)CD=5m.连接OB.求这座石拱桥主桥拱的半径.(精确到1m).
 15. 如图,为的直径,弦于点 , 连接 , , , 为中点,且.
15. 如图,为的直径,弦于点 , 连接 , , , 为中点,且. (1)、求的长;(2)、当时,
(1)、求的长;(2)、当时,① ;
②求阴影部分的周长和面积.
四、综合题

