2023-2024学年湘教版初中数学九年级下册 2.1 圆的对称性同步分层训练培优题
试卷更新日期：2024-01-27 类型：同步测试
一、选择题
-
1. 若⊙P的半径为13，圆心P的坐标为（5， 12 )，则平面直角坐标系的原点O与⊙P的位置关系是（ )
A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定2. 如图，在中， ， 则劣弧的度数为（ ）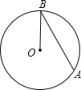
A、106° B、126° C、74° D、53°3. 如图，已知OA，OB， OC是⊙O的半径，连结BC，交OA于点D，设∠ADB=a，∠OBC=p，∠AOC=y， 则（ ）
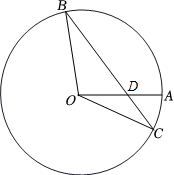A、a+2β-y= 180° B、a+β+y= 180° C、2a-β+y=180° D、3a-2β+y=180°4. 如图，抛物线 与 轴交于 两点， 是以点 为圆心， 为半径的圆上的动点， 是线段 的中点，连接 ，则线段 的最小值是（ ）
A、 B、 C、 D、5. 如图，矩形ABCD，AD=1，CD=2，点P为边CD上的动点（P不与C重合），作点P关于BC的对称点Q，连结AP，BP和BQ，现有两个结论：①若DP≥1，当△APB为等腰三角形时，△APB和△PBQ一定相似；②记经过P，Q，A三点的圆面积为S，则4π≤S＜。下列说法正确的是（ ）
A、①对②对 B、①对②错 C、①错②对 D、①错②错6. 一个点到圆的最大距离为11cm，最小距离为5cm，则圆的半径为（ ）A、16cm或6cm， B、3cm或8cm C、3cm D、8cm7. 已知矩形ABCD的边AB＝15，BC＝20，以点B为圆心作圆，使A，C，D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是 （ ）
A、r＞15 B、15＜r＜20 C、15＜r＜25 D、20＜r＜258. 如图点A，D，G，B在半圆上，四边形ABOC，DEOF，HMNO均为矩形，设BC=a， EF=b， NH=c，则下列说法正确的是（ ）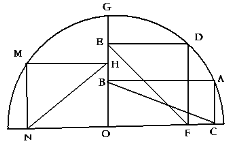
A、a＞b＞c B、a＝b＝c C、c＞a＞b D、b＞c＞a二、填空题
-
9. 若点在二次函数的图像上，以P为圆心，为半径的圆与y轴相交，则n的取值范围是.10. 如图，点A，B，C在⊙O上， ， ， 则.
11. 如图，数学知识在生产和生活中被广泛应用．下列实例所应用的最主要的几何知识为：①射击时，瞄准星的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；
②车轮做成圆形，应用了“圆上各点到圆心的距离相等”；
③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；
④地板砖可以做成矩形，应用了“矩形对边相等”．
上述说法正确的是 ． （填序号）
12. 如图，抛物线与x轴交于A，B两点，点C的坐标为 ， ⊙C半径为4，P是⊙C上一动点，Q是线段PB的中点，连接OQ．则线段OQ的最大值是 ．
13. 如图，在中， ， 点D为的中点，点E是线段上一动点，把沿直线翻折，点A的对称点是F，连结 ， 若 ， 则的长是.
三、解答题
-
14. 如图，A 城气象台测得台风中心在A城正西方向300km的B处，以km/h的速度向北偏东60°的BF方向移动．已知距台风中心200km的范围内是受到台风影响的区域．
(1)、A城是否受到这次台风的影响？为什么？(2)、若A城受到台风影响，则A城将遭受到这次台风影响的时间有多长？15.（1）已知⊙O的直径为10cm，点A为⊙O外一定点，OA=12cm，点P为⊙O上一动点，求PA的最大值和最小值．
（2）如图：
=
， D、E分别是半径OA和OB的中点．求证：CD=CE．
四、综合题
-
16. 如图，在平面直角坐标系中，A（0，4）、B（4，4）、C（6，2）．设经过A、B、C三点的圆弧所在的圆的圆心为点M，
(1)、点M的坐标为；(2)、点D（5，﹣2）在⊙M （填“内”、“外”、“上”）．17. 如图
(1)、【问题发现】如图1，P是半径为2的⊙O上一点，直线m是⊙O外一直线，圆心O到直线m的距离为3，PQ⊥m于点Q，则PQ的最大值为；(2)、【问题探究】如图2，将两个含有30°角的直角三角板的60°角的顶点重合（其中∠A==30°，∠C=∠C'=90°），绕点B旋转 ， 当旋转至CC′=4时，求的长；(3)、【问题解决】如图3，点O为等腰RtABC的斜边AB的中点，AC=BC=5 ， OE=2，连接BE，作RtBEF，其中∠BEF=90°，tan∠EBF= ， 连接AF，求四边形ACBF的面积的最大值．