湘教版数学九年级下册 2.1 圆的对称性同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 已知的半径为 , 点在外,则的长为( )A、 B、 C、 D、2. 用尺规作图作一个已知角的平分线的示意图如图如示,以O为圆心,以适当长度为半径作弧,分别交、于M、N点,再分别以M、N点为圆心,以大于的长度为半径作弧,两弧交于C点,连接 , 则能说明的依据是( )
 A、 B、 C、 D、角平分线上的点到角两边的距离相等3. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )
A、 B、 C、 D、角平分线上的点到角两边的距离相等3. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )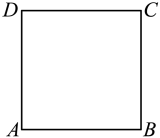 A、点在外 B、点在内 C、点在上 D、无法确定4. 在如图所示的6×6的方格中,每个小方格的边长都为1,有M , N , O , P , Q五个格点,若以O为圆心,为半径作圆,则在⊙O外的是( )
A、点在外 B、点在内 C、点在上 D、无法确定4. 在如图所示的6×6的方格中,每个小方格的边长都为1,有M , N , O , P , Q五个格点,若以O为圆心,为半径作圆,则在⊙O外的是( ) A、点M B、点N C、点P D、点Q5. 如图,A,B,C是某社区的三栋楼,若在AC中点D处建一个5G基站,其覆盖半径为300 m,则这三栋楼中在该5G基站覆盖范围内的是( )
A、点M B、点N C、点P D、点Q5. 如图,A,B,C是某社区的三栋楼,若在AC中点D处建一个5G基站,其覆盖半径为300 m,则这三栋楼中在该5G基站覆盖范围内的是( ) A、A,B,C都不在 B、只有B C、只有A,C D、A,B,C6. 如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )
A、A,B,C都不在 B、只有B C、只有A,C D、A,B,C6. 如图,在Rt△ABC中,∠ACB=90°,AC=3,以点C为圆心,CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为( )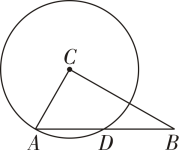 A、 B、3 C、9 D、67. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( )
A、 B、3 C、9 D、67. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 若⊙O的半径为3,点P为平面内一点,OP=2,那么点P在⊙O(填“上”、“内部”或“外部”)9. 已知⊙O的半径为5,PO=4,则点P在 (填圆内,圆上或圆外).10. 已知的半径是 , 点与圆心的距离分别为 . 则点在 , 点在 , 点在 .11. 如图,在△ABC中,∠ACB=90°,AB=5,BC=4,以点A为圆心,r为半径作圆,当点C在⊙A内且点B在⊙A外时,r的值可能是 (写出一个即可).

三、解答题
-
12. 如图,矩形ABCD的边AB=3cm,AD=4cm.以点A为圆心,4cm为半径作⊙A,试判断点B,C,D与⊙A的位置关系.
 13. 如图,长方形ABCD的边AB=3,AD=4.
13. 如图,长方形ABCD的边AB=3,AD=4. (1)、以点A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?(2)、若以点A为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围.
(1)、以点A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?(2)、若以点A为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围.四、综合题
-
14. 如图,上午9: 00,一轮船在点A处接到警报,台风中心位于轮船正南方向100海里的点B处,轮船以10海里/时的速度由西向东航行,台风中心以20海里/时的速度由南向北移动,距台风中心50海里(包括边界)的圆形区域都属于台风影响区.
 (1)、若轮船继续向东航行t小时至A1 , 此时台风中心位于B1 , 用含t的代数式表示=;(2)、若轮船不改变航行速度和方向,求轮船开始受台风影响的时刻.15. 如图,△ABC中,∠ACB=90°,AC=6,BC=8,点O是AB的中点.
(1)、若轮船继续向东航行t小时至A1 , 此时台风中心位于B1 , 用含t的代数式表示=;(2)、若轮船不改变航行速度和方向,求轮船开始受台风影响的时刻.15. 如图,△ABC中,∠ACB=90°,AC=6,BC=8,点O是AB的中点.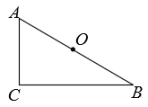 (1)、若以点O为圆心,以R为半径作⊙O,且点A,B,C都在⊙O上,求R的值;(2)、若以点B为圆心,以r为半径作⊙B,且点O,A,C中有两个点在⊙B内,有一个点在⊙B外,求r的取值范围.
(1)、若以点O为圆心,以R为半径作⊙O,且点A,B,C都在⊙O上,求R的值;(2)、若以点B为圆心,以r为半径作⊙B,且点O,A,C中有两个点在⊙B内,有一个点在⊙B外,求r的取值范围.