湘教版数学九年级下册 1.5 二次函数的应用同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 某题市以每件10元的价格购进一种文具.经过市场调查发现,该文具每天的销售数量y(件)与销售单价x(元)()之间满足 , 则销售这种文具每天可得( )A、最大利润150元 B、最大利润128元 C、最小利润150元 D、最小利润12022. 如图,一个移动喷灌架喷射出的水流可以近似地看成抛物线,喷水头的高度(即OB的长度)是1米.当喷射出的水流距离喷水头2米时,达到最大高度米,水流喷射的最远水平距离OC是( )
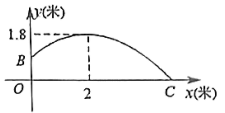 A、6米 B、5米 C、4米 D、1米3. 如图,有一抛物线形拱桥,当拱顶离水面时,水面宽 , 当水面宽增加时,则水面应下降的高度是( )
A、6米 B、5米 C、4米 D、1米3. 如图,有一抛物线形拱桥,当拱顶离水面时,水面宽 , 当水面宽增加时,则水面应下降的高度是( )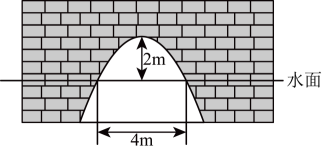 A、 B、 C、 D、4. 如图,用一根60cm的铁丝制作一个“日”字型框架 , 铁丝恰好全部用完,则该“日”字型框架面积的最大值为( )
A、 B、 C、 D、4. 如图,用一根60cm的铁丝制作一个“日”字型框架 , 铁丝恰好全部用完,则该“日”字型框架面积的最大值为( ) A、150 B、 C、 D、5. 如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD , 那么CD宽为( )
A、150 B、 C、 D、5. 如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD , 那么CD宽为( ) A、4米 B、10米 C、4米 D、12米6. 某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时,平均每天能售出8件,而当销售价每降低2元时,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价为( )A、21元 B、22元 C、23元 D、24元7. 如图,在中, , , 于点点从点出发,沿的路径运动,运动到点停止,过点作于点 , 作于点设点运动的路程为 , 四边形的面积为 , 则能反映与之间函数关系的图象是( )
A、4米 B、10米 C、4米 D、12米6. 某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时,平均每天能售出8件,而当销售价每降低2元时,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价为( )A、21元 B、22元 C、23元 D、24元7. 如图,在中, , , 于点点从点出发,沿的路径运动,运动到点停止,过点作于点 , 作于点设点运动的路程为 , 四边形的面积为 , 则能反映与之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,边长为的等边和边长为的等边 , 它们的边 , 位于同一条直线上,开始时,点与点重合,固定不动,然后把自左向右沿直线平移,移出外点与点重合停止,设平移的距离为 , 两个三角形重合部分的面积为 , 则关于的函数图象是( )
8. 如图,边长为的等边和边长为的等边 , 它们的边 , 位于同一条直线上,开始时,点与点重合,固定不动,然后把自左向右沿直线平移,移出外点与点重合停止,设平移的距离为 , 两个三角形重合部分的面积为 , 则关于的函数图象是( )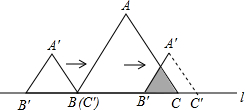 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 某广场要建一个圆形喷水池,计划在池中心位置竖直安装一根带有喷水头的水管,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m(如图).若水柱落地处离池中心的水平距离也为3m,则水管的设计高度应为m.
 10. 已知二次函数的顶点在第一象限.
10. 已知二次函数的顶点在第一象限.⑴点的坐标是 . (用含的式子表示)
⑵若抛物线与轴交于两点,连接 , 则的值是 .
11. 原地正面掷实心球是北京市初中学业水平考试体育现场考试的选考项目之一.实心球被掷出后的运动路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系 , 实心球从出手到着陆的过程中,它的竖直高度(单位:m)与水平距离(单位:m)近似满足函数关系 .
小明进行了两次掷实心球训练.
1 第一次训练时,实心球的水平距离与竖直高度的几组数据如下:
水平距离x/m
0
1
2
3
4
5
6
竖直高度y/m
根据上述数据,实心球竖直高度最大值是m;
⑵第二次训练时,实心球的竖直高度与水平距离近似满足函数关系 , 记第一次训练实心球的着陆点的水平距离为 , 第二次训练实心球的着陆点的水平距离为 , 则(填“”,“”或“”).
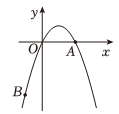
12. 如图,抛物线与x轴的正半轴交于点A , 点在该抛物线上.⑴m的值为;
⑵连接AB , P是直线AB上的动点,将点P向左平移5个单位长度得到点Q . 若线段PQ与抛物线只有一个公共点,则点P的横坐标x的取值范围为。
 13. 如图,抛物线与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是.
13. 如图,抛物线与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是.
三、解答题
-
14. 抛物线:与轴交于点 , , 与轴交于点 , 顶点为 .
 (1)、求抛物线的解析式和顶点的坐标.(2)、如图,在坐标平面上放置一透明矩形胶片 , 并在胶片上描画出抛物线在矩形胶片内部(含边界)的一段,记为 , 把该胶片绕点顺时针旋转 , 得到矩形胶片以及对应的图像 .
(1)、求抛物线的解析式和顶点的坐标.(2)、如图,在坐标平面上放置一透明矩形胶片 , 并在胶片上描画出抛物线在矩形胶片内部(含边界)的一段,记为 , 把该胶片绕点顺时针旋转 , 得到矩形胶片以及对应的图像 .①求旋转过程中扫过的面积;
②求图像所在的抛物线的解析式.
15. 排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生第一次在处将球垫偏,之后又在A、两处先后垫球,球沿抛物线运动(假设抛物线、、在同一平面内),最终正好在处垫住,处离地面的距离为1米.如图所示,以为坐标原点1米为单位长度建立直角坐标系,轴平行于地面水平直线 , 已知点 , 点的横坐标为 , 抛物线表达式为和抛物线表达式为 .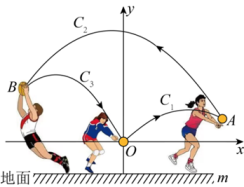 (1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?
(1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?四、综合题
-
16. 如图,抛物线与轴交于点 , 两点,与轴交于点 , 抛物线的对称轴是直线 .
 (1)、求抛物线的解析式及点坐标;(2)、如图1,连接 , 在对称轴上找一点 , 且点在第一象限内,使得是以为底角的等腰三角形,求点的坐标;(3)、如图2,第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 当的值最大时,求点的坐标,并求出这个最大值。17. 如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C , 点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接PA , PF , AF .
(1)、求抛物线的解析式及点坐标;(2)、如图1,连接 , 在对称轴上找一点 , 且点在第一象限内,使得是以为底角的等腰三角形,求点的坐标;(3)、如图2,第一象限内的抛物线上有一动点 , 过点作轴,垂足为 , 连接交于点 . 当的值最大时,求点的坐标,并求出这个最大值。17. 如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C , 点P为x轴上方抛物线上的动点,点F为y轴上的动点,连接PA , PF , AF .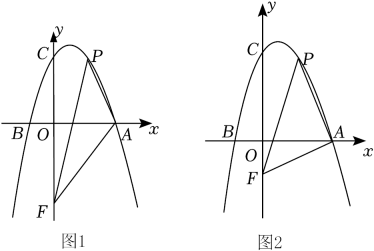 (1)、求该抛物线所对应的函数解析式;(2)、如图1,当点F的坐标为(0,﹣3),过点P作x轴的垂线,交线段AF于点D , 求线段PD长度的最大值;(3)、如图2,是否存在点F , 使得△AFP是以点A为直角顶点的等腰直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.
(1)、求该抛物线所对应的函数解析式;(2)、如图1,当点F的坐标为(0,﹣3),过点P作x轴的垂线,交线段AF于点D , 求线段PD长度的最大值;(3)、如图2,是否存在点F , 使得△AFP是以点A为直角顶点的等腰直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.