2023-2024学年湘教版初中数学九年级下册 1.5 二次函数的应用同步分层训练基础题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 用绳子围成周长为10（m）的矩形，记矩形的一边长为x（m），面积为S（m²）．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（）

A、一次函数关系 B、二次函数关系 C、反比例函数关系 D、正比例函数关系

查看试题解析
2. 在一次炮弹发射演习中，记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为 $y = \frac{1}{5} x^{2} + 10 x$ ，当炮弹落到地面时，经过的时间为（）

A、40秒 B、45秒 C、50秒 D、55秒

查看试题解析
3. 已知实心球运动的高度y（m）与水平距离x（m）之间的函数关系是y＝-（x-1）²+4，则该同学此次投掷实心球的成绩是（）

A、2m B、3m C、3.5m D、4m

查看试题解析
4. 据省统计局公布的数据，合肥市2023年第一度GDP总值约为26千亿元人民币，若我市第三季度GDP总值为y千亿元人民币，平均每个季度GDP增长的百分率为x ，则y关于x的函数表达式是（）

A、 $y = 2.6 (1 + 2 x)$ B、 $y = 2.6 {(1 - x)}^{2}$ C、 $y = 2.6 {(1 + x)}^{2}$ D、 $y = 2.6 + 2.6 (1 + x) + 2.6 {(1 + x)}^{2}$

查看试题解析
5. 在特定条件下，篮球赛中进攻球员投球后，篮球的运行轨迹是开口向下的抛物线的一部分．“盖帽”是一种常见的防守手段，防守队员在篮球上升阶段将球拦截即为“盖帽”，而防守队员在篮球下降阶段将球拦截则属“违规”．对于某次投篮而言，如果忽略其他因素的影响，篮球处于上升阶段的水平距离越长，则被“盖帽”的可能性越大，收集几次篮球比赛的数据之后，某球员投篮可以简化为下述数学模型：如图所示，该球员的投篮出手点为P，篮框中心点为Q，他可以选择让篮球在运行途中经过A，B，C，D四个点中的某一点并命中Q，忽略其他因素的影响，那么被“盖帽”的可能性最大的线路是（）

A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Ω

查看试题解析
6. 如果一个球从地面竖直向上弹起时的速度为10米/秒，经过t（秒）时球距离地面的高度h（米）适用公式h=10t-5t² ，那么球弹起后又回到地面所花的时间t是（）

A、5秒 B、10秒 C、1秒 D、2秒

查看试题解析
7. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是y= $- \frac{1}{12}$ （x-10）（x+4），则铅球推出的距离OA=（）

A、14m B、10m C、7m D、4m

查看试题解析
8. 如图所示，一座抛物线形的拱桥在正常水位时，水面AB宽为20米，拱桥的最高点O到水面AB的距离为4米．如果此时水位上升3米就达到警戒水位CD，那么CD宽为（　　）

A、4 $\sqrt{5}$ 米 B、10米 C、4 $\sqrt{6}$ 米 D、12米

查看试题解析

二、填空题

9. 在中考体育训练期间，小宇对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系式为y=- $\frac{1}{10}$ x²+ $\frac{3}{5}$ x+ $\frac{8}{5}$ ，由此可知小宇此次实心球训练的成绩为米.

查看试题解析
10. 如图所示，桥拱是抛物线形，其函数解析式是y＝﹣ $\frac{1}{4}$ x² ，当水位线在AB位置时，水面宽为12米，这时水面离桥顶的高度h是米．

查看试题解析
11. 以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt﹣4.9t² ．现将某弹性小球从地面竖直向上抛出，初速度为v₁ ，经过时间t₁落回地面，运动过程中小球的最大高度为h₁；小球落地后，竖直向上弹起，初速度为v₂ ，经过时间t₂落回地面，运动过程中小球的最大高度为h₂ ．若h₁＝1.21h₂ ，则t₁：t₂＝．

查看试题解析
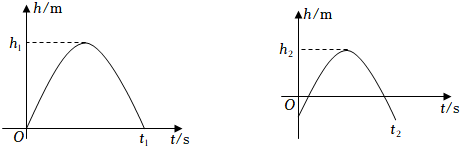12. 已知点 $M (a ， b)$ 是抛物线 $y = x^{2} - 4 x + 5$ 上一动点．

(1)、当点M到y轴的距离不大于1时，b的取值范围是；

(2)、当点M到直线 $x = m$ 的距离不大于 $n (n > 0)$ 时，b的取值范围是 $5 \leq b \leq 10$ ，则 $m + n$ 的值为．

查看试题解析
13. 某服装店购进单价为15元童装若干件，销售一段时间后发现：当销售价为25元时平均每天能售出8件，而当销售价每降低2元，平均每天能多售出4件，当每件的定价为元时，该服装店平均每天的销售利润最大．

查看试题解析

三、解答题

14. 某宾馆有40个房间供游客居住，当每个房间每天的定价为200元时，房间会全部住满：当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．

(1)、若每个房间定价增加30元，则这个宾馆这一天的利润为多少元？

(2)、若宾馆某一天获利8400元，则房价定为多少元？

(3)、房价定为多少时，宾馆的利润最大？

查看试题解析
15. 毛泽东故居景区有一商店销售一种纪念品，这种商品的成本价为10元/件，已知销售价不低于成本价，且物价部门规定这种商品的销售价不高于20元/件，市场调查发现，该商品每天的销售量y（件）与销售价x（元/件）之间的函数关系如图所示．

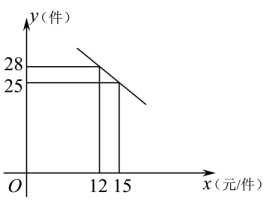(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、求每天的销售利润W（元）与销售价x（元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

查看试题解析

四、综合题

16. 商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施，经调查发现，每件商品每降价1元，商场每天可多售出2件，设每件商品降低x元据此规律，请回答：

(1)、商场日销售量增加件，每件商品盈利元（用含x的代数式表示）；

(2)、在上述条件不变，销售正常的情况下，设商场日盈利y元，求y与x的函数关系式；

(3)、在（2）的条件下，每件商品降价多少元时，商场日盈利最高？

查看试题解析
17. 某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙（墙的长度为10m），另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1：2的矩形，已知栅栏的总长度为24m，设较小矩形的宽为xm（如图）.

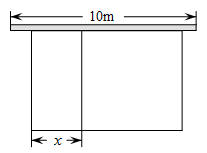(1)、若矩形养殖场的总面积为36 $m^{2}$ ，求此时x的值；

(2)、当x为多少时，矩形养殖场的总面积最大？最大值为多少？

查看试题解析