2023-2024学年湘教版初中数学九年级下册 1.3 不共线三点确定二次函数的表达式同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 抛物线 $y = \frac{1}{2} x^{2} - b x + 3$ 图像经过点 $(- 2 ， 1)$ ，则 $b$ 的值为（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 已知函数y＝ax²（a≠0）经过点（-1，2），则必经过点（）

A、（1，-2） B、（1，2） C、（2，-1） D、（2，1）

查看试题解析
3. 已知某抛物线与二次函数 $y = - 5 x^{2}$ 的图象的开口大小相同，开口方向相反，且顶点坐标为（1，2023），则该抛物线对应的函数表达式为（　　）

A、 $y = 5 {(x - 1)}^{2} + 2023$ B、 $y = - 5 {(x - 1)}^{2} + 2023$ C、 $y = 5 {(x + 1)}^{2} + 2023$ D、 $y = - 5 {(x + 1)}^{2} + 2023$

查看试题解析
4. 如图，在平面直角坐标系中，点A、E在抛物线 $y = a x^{2}$ 上，过点A、E分别作y轴的垂线，交抛物线于点B、F，分别过点E、F作x轴的垂线交线段AB于两点C、D．当点 $E (2 ， 4)$ ，四边形 $C D F E$ 为正方形时，则线段 $A B$ 的长为（　　）

A、4 B、 $4 \sqrt{2}$ C、5 D、 $5 \sqrt{2}$

查看试题解析
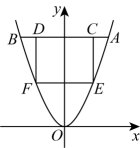5. 抛物线 $y = a x^{2} + b x + c$ 上部分点的横坐标 $x$ ，纵坐标 $y$ 的对应值如表 $.$ 下列结论不正确的是（）
          $x$
          $- 2$
          $- 1$
          $0$
          $1$
          $y$
          $0$
          $4$
          $6$
          $6$

A、抛物线的开口向下 B、抛物线与 $x$ 轴的一个交点坐标为 $(2 ， 0)$ C、抛物线的对称轴为直线 $x = \frac{1}{2}$ D、函数 $y = a x^{2} + b x + c$ 的最大值为 $\frac{25}{4}$

查看试题解析
6. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+3（a＜0）交x轴于A，B两点（B在A左侧），交y轴于点C，且CO＝AO，分别以BC，AC为边向外作正方形BCDE、正方形ACGH，记它们的面积分别为S₁ ， S₂ ， △ABC面积记为S₃ ，当S₁+S₂＝6S₃时，b的值为（　　）

A、 $- \frac{1}{2}$ B、 $- \frac{2}{3}$ C、 $- \frac{3}{4}$ D、 $- \frac{4}{3}$

查看试题解析
7. 如图，抛物线与x轴交于点A，B，与y轴交于点G，正方形 $C D E F$ 的边 $C D$ 在x轴上，E，F在抛物线上，连结 $G A$ ， $G B$ ， $△ A B G$ 是正三角形， $A B = 2$ ，则阴影部分的面积为（）

A、 $\sqrt{3} - \frac{1}{2}$ B、 $3 - \sqrt{3}$ C、 $2 - \frac{\sqrt{2}}{2}$ D、 $2 - \frac{\sqrt{3}}{3}$

查看试题解析
8. 如图，在平面直角坐标系中，矩形O ABC的点B坐标为（8， 6），点A在x轴上，点C在y轴上.点D是边AB上的动点，连接OD，作点A关于线段OD的对称点A'.已知一条抛物线y=ax²+bx+c（a≠0）经过O，A'，A三点，且点A'恰好是抛物线的顶点，则b的值为（）

A、- $\sqrt{3}$ B、2 $\sqrt{3}$ C、-2 $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析

二、填空题

9. 已知二次函数的图象与x轴的两个交点A ， B关于直线 $x = - 1$ 对称，且 $A B = 6$ ，顶点在函数 $y = 2 x$ 的图象上，则这个二次函数的表达式为．

查看试题解析
10. 将抛物线y=2(x-3)²+m先向右平移3个单位，再向上平移1个单位后恰好经过点(2，3)，则m的值是.

查看试题解析
11. 对于一个函数，自变量x取a时，函数值y也等于a，则称a是这个函数的不动点．已知二次函数 $y = x^{2} + 3 x + m$ ，

(1)、若2是此函数的不动点，则m的值为．

(2)、若此函数有两个相异的不动点a，b，且 $a < 1 < b$ ，则m的取值范围为．

查看试题解析
12. 已知抛物线 $y = a x^{2} + b x + 3$ 的图象与x轴相交于点A和点 $B (1 ， 0)$ ，与y轴交于点C，连接 $A C$ ，有一动点D在线段 $A C$ 上运动，过点D作x轴的垂线，交抛物线于点E，交x轴于点F， $A B = 4$ ，设点D的横坐标为m．连接 $A E ， C E$ ，则 $△ A C E$ 的最大面积为．

查看试题解析
13. 如图，抛物线 $C_{1}$ ： $y = x^{2} + 2 x - 3$ 与抛物线 $C_{2}$ ： $y = a x^{2} + b x + c$ 组成一个开口向上的“月牙线”，抛物线 $C_{1}$ 和抛物线 $C_{2}$ 与x轴有着相同的交点A、B（点B在点A右侧），与y轴的交点分别为C、D．如果 $B D = C D$ ，那么抛物线 $C_{2}$ 的表达式是．

查看试题解析

三、解答题

14. 若抛物线的顶点坐标是A（-1，-3），并且抛物线经过点B坐标为（1，-1）.

(1)、求出该抛物线的关系式；

(2)、当x满足什么条件时，y随x的增大而增大

查看试题解析
15. 如图，抛物线 $y = x^{2} + b x + c$ 与 $x$ 轴交于点 $A$ ， $B$ ，与 $y$ 轴交于点 $C$ ，点 $A$ 的坐标为 $(- 1，0)$ ，点 $B$ 的坐标为 $(3，0)$ ．

(1)、求抛物线的表达式；

(2)、当 $a - 2 \leq x \leq a + 1$ 时，抛物线有最小值 $5$ ，求 $a$ 的值．

查看试题解析

四、综合题

16. 已知二次函数y＝2x²+bx+c（b，c是常数）

(1)、若A（1，0），B（0，4）两点在该二次函数图象上，求二次函数的表达式．

(2)、若二次函数的表达式可以写成y＝2（x-h）²-2的形式（h是常数），求b+c的最小值．

(3)、若二次函数的表达式还可以写成y＝2（x-m）（x-m-k），它的图象与x轴交于A，B两点，一次函数y＝kx+b的图象经过点A，且与二次函数的图象交于另一点C．是否存在实数k，使得△ABC是以AB为腰的等腰三角形，如果存在，求出k的值；如果不存在，请说明理由．

查看试题解析
17. 如图，直线AB与抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 交于 $A (- 4 ， 0)$ 、 $B (2 ， 6)$ 两点，与y轴交于点C，点D为线段AB上一点，连接OD、OB.

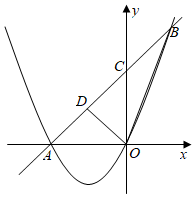(1)、求抛物线的解析式；

(2)、若OD将 $△ A O B$ 分成面积相等的两部分，求点D的坐标；

(3)、在平面坐标内是否存在点P，使得以A、O、B、P为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析

$x$	$- 2$	$- 1$	$0$	$1$
$y$	$0$	$4$	$6$	$6$