2023-2024学年湘教版初中数学九年级下册 1.2 二次函数的图像与性质同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 二次函数 $y = a x^{2} - 2 x - 3 (a < 0)$ 的图象一定不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限.

查看试题解析
2. 已知抛物线 $y = a x^{2} - 4 a x + c$ 经过点 $(- 1 ， 2)$ ，则该抛物线必然还经过点（）

A、 $(- 1 ， - 2)$ B、 $(- 3 ， 2)$ C、 $(3 ， 2)$ D、 $(5 ， 2)$

查看试题解析
3. 如图，二次函数 $y = a x^{2} + x - 6$ 的图象与x轴交于 $A (- 3 ， 0)$ ， B两点，下列说法正确的是（）

A、抛物线的对称轴为直线 $x = 1$ B、抛物线的顶点坐标为 $(- \frac{1}{2} ， - 6)$ C、A，B两点之间的距离为5 D、当 $x < - 1$ 时，y的值随x值的增大而增大

查看试题解析
4. 二次函数y＝ax²+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，对称轴为 $x = 1$ ，下列结论中正确的是（）

A、 $a b > 0$ B、 $b = 2 a$ C、 $4 a + 2 b + c < 0$ D、 $a + c < b$

查看试题解析
6. 设k为非负实数，且方程 $x^{2}$ -2kx+4=0的两实数根为a，b，则 ${（ a - 1 ）}^{2}$ + ${（ b - 1 ）}^{2}$ 的最小值为（）

A、-7 B、-6 C、2 D、4

查看试题解析
7. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示．下列结论正确的有（）
① $a b c < 0$ ；② $2 a + b = 0$ ；③ $m$ 为任意实数时， $a + b \leq m (a m + b)$ ；④ $a - b + c > 0$ ；⑤若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ ；则 $x_{1} + x_{2} = 2$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，已知二次函数y＝ax²+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝1．下列结论：①abc＞0；②4a+2b+c＞0；③4ac﹣b²＞8a；④ $\frac{1}{3} < a < \frac{2}{3}$ ；⑤b＞c ．其中含所有正确结论的选项是（　　）

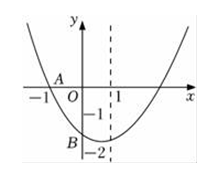A、①②③ B、②③④ C、①④⑤ D、①③④⑤

查看试题解析

二、填空题

9. 在二次函数y=ax² $-$ 2ax+b中，当0≤x≤3时， $-$ 2≤y≤6，则ab= ．

查看试题解析
10. 如图，平面直角坐标系中有两个二次函数的图象，其顶点P ， Q皆在x轴上，且有一水平线与两图象相交于A、B、C、D四点，各点位置如图所示，若 $A B = 10$ ， $B C = 5$ ， $C D = 6$ ，则PQ的长度为.

查看试题解析
11. 关于x的二次函数y=ax²－4ax+b中，当1≤x≤4时，-3≤y≤5. 则b-4a的值为

查看试题解析
12. 二次函数y= $x^{2}$ -2ax+a在0≤x≤2上有最小值-6，则a的值为.

查看试题解析
13. 已知二次函数 $y = a x^{2} + b x + c$ ，当 $- 1 \leq x \leq 1$ 时， $- 1 \leq y \leq 1$ .

(1)、若 $b = 0$ ， $c = 1$ ，则 $a =$ .

(2)、若抛物线 $y = a x^{2} + b x + c$ 经过点 $A (1 ， - 1)$ 和点 $B (- 1 ， 1)$ ，则 $a$ 的取值范围是.

查看试题解析

三、解答题

14. 已知关于 $x$ 的二次函数 $y = x^{2} + (k - 1) x + 3$ ，其图象经过点 $(1 ， 8)$ ．

(1)、求 $k$ 的值，并写出二次函数的关系式；

(2)、求出二次函数图象的顶点坐标．

查看试题解析
15. 已知：如图，在矩形ABCD中，AB＝8，BC＝5．在AD上取一点E ，点F是AB边上的一个动点，以EF为一边作四边形EFMN ，使点N落在CD边上，点M落在矩形ABCD内或其边上，若AF＝x ， △BFM的面积为S ．

(1)、当AE＝2，四边形EFMN是正方形时，求x的值为；

(2)、当AE＝2，四边形EFMN是菱形时，求S与x的函数关系式；

(3)、当四边形EFMN是矩形时且矩形的两邻边EF：EN＝2：1，请直接写出S与x的函数关系式；并指出S的最大值．

查看试题解析

四、综合题

16. 如图，一块材料的形状是锐角三角形ABC ，边BC=120mm ，高AD=80mm ，把它加工成矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，设EG=x mm ， EF=y mm ．

(1)、写出x与y的关系式；

(2)、用S表示矩形EGHF的面积，某同学说当矩形EGHF为正方形时S最大，这个说法正确吗？说明理由，并求出S的最大值．

查看试题解析
17. 如图，直线 $y = - \frac{2}{3} x + c$ 与x轴交于点A（3，0），与y轴交于点B，抛物线 $y = - \frac{4}{3} x_{}^{2} + b x + c$ 经过点A，B．

(1)、求点B的坐标和抛物线的解析式；

(2)、M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．
①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标.
②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点“．请直接写出使得M，P，N三点成为“共谐点”的m的值．

查看试题解析