2023-2024学年湘教版初中数学九年级下册 1.2 二次函数的图像与性质同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、y=﹣(x﹣1)2+3 B、y=﹣(x+1)2+3 C、y=﹣(x+1)2﹣3 D、y=﹣(x﹣1)2﹣32. 关于x的二次函数在y轴右侧y随x的增大而减小,则a的范围为( )A、 B、 C、 D、3. 已知二次函数y=-x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )A、b≥-1 B、b≤-1 C、b≥1 D、b≤14. 抛物线的顶点坐标是( )A、 B、 C、 D、5. 二次函数y=(x﹣1)2﹣3的最小值是( )A、2 B、1 C、﹣2 D、﹣36. 把方程x2﹣8x+3=0化成(x+m)2=n的形式,则m,n的值是( )A、4,13 B、﹣4,19 C、﹣4,13 D、4,197. 已知二次函数y=a(x+1)(x-m)(a≠0,1<m<2),当x<-1时,y随x的增大而增大,则下列结论正确的是( )
①当x>2时,y随x的增大而减小;②若图象经过点(0,1),则-1<a<0;
③若(-2022,y1),(2022,y2)是函数图象上的两点,则y1<y2:
④若图象上两点对一切正数n,总有y1>y2 , 则 .
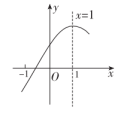
A、①② B、①③ C、①②③ D、①③④8. 已知二次函数( , , 为常数,)的部分图象如图所示,对称轴为直线 , 且与x轴的一个交点在点和之间.下列四个结论:①;②若点、在此抛物线上,则;③;
④对于任意实数m,总有 .
其中正确的结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 在函数中,当x时,y随x的增大而减小.10. 如果抛物线向下平移2个单位,所得到的抛物线是 .11. 已知抛物线 (a<0)过A(-2,0)、O(0,0)、B(-3, )、C(3, )四点,则 与 的大小关系是12. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
x
…
-1
0
1
2
…
y=ax2+bx+c
…
m
-1
-1
n
t
…
且当x=-时,与其对应的函数值y>0,有下列结论:①abc>0;②当x>1时,y随x的增大而减小;③关于x的方程ax2+bx+c=t的两个根是和1-;④m+n> . 其中正确的结论是 . (填写序号)
13. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.下列四个结论:①;②;③函数的最大值为;④若关于x的方程无实数根,则.其中正确的是(填写序号).
三、解答题
-
14. 某学生为了描点作出函数y=ax2+bx+c(a≠0)的图象,取了自变量的7个值,x1<x2<…<x7且x2﹣x1=x3﹣x2=…=x7﹣x6 , 分别算出对应的y的值,列出如表;
X
x1
x2
x3
x4
x5
x6
x7
y
51
107
185
285
407
549
717
但由于粗心算出了其中一个y的值,请指出算错的是哪一个值?正确的值是多少?并说明理由.
15. 如图,已知抛物线y=x2上有一点A , A点的横坐标是-1,过点A作AB∥x轴,交抛物线于另一点B , 求△AOB的面积.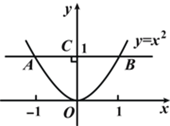
四、综合题