2023-2024学年湘教版初中数学九年级下册 1.1 二次函数同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 下列函数中，y一定是x的二次函数的是（）

A、 $y = a x^{2} + b x + c$ B、 $y = 50 + x^{2}$ C、 $y = x + 2$ D、 $y = {(x + 1)}^{2} - x^{2}$

查看试题解析
2. 若 $y = (m - 2) x^{m^{2} - 2} - x + 1$ 是二次函数，则m的值是（）

A、4 B、2 C、-2 D、-2或2

查看试题解析
3. 如图，矩形ABCD中，BC＝4，AB＝3，点P是BC边上的动点（点P不与点B、C重合）．现将ΔPCD沿PD翻折，得到ΔPC’D ，作∠BPC＇的平分线，交AB于点E ．设BP＝x ， BE＝y ，则下列符合题意的函数关系式是（）

A、y＝－ $\frac{1}{3}$ x² ＋ $\frac{4}{3}$ x（0＜x＜4） B、y＝－ $\frac{1}{3}$ x²－ $\frac{4}{3}$ x（0＜x＜4） C、y＝－ $\frac{1}{2}$ x² ＋2x（0＜x＜4） D、y＝ $\frac{1}{2}$ x² －2x（0＜x＜4）

查看试题解析
4. 某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A、50（1+x²）=196 B、50+50（1+x²）=196 C、50+50（1+x）+50（1+x）²=196 D、50+50（1+x）+50（1+2x）=196

查看试题解析
5. 下列实际问题中的y关于x的函数表达式是二次函数的为（）.

A、正方体集装箱的体积y m³ ，棱长x m B、高为14 m的圆柱形储油罐的体积y m³ ，底面圆半径x m C、妈妈买烤鸭花费86元，烤鸭的质量为y千克，单价为x元/千克 D、小莉驾车以108km/h的速度从南京出发到上海，行驶xh，距上海y km

查看试题解析
6.
如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是( )

A、 $y = \frac{2}{25} x^{2}$ B、 $y = \frac{4}{25} x^{2}$ C、 $y = \frac{2}{5} x^{2}$ D、 $y = \frac{4}{5} x^{2}$

查看试题解析
7.
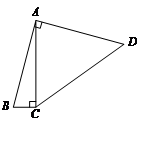
如图，半圆O的直径AB=4，与半圆O内切的动圆O₁与AB切于点M，设⊙O₁的半径为y，AM=x，则y关于x的函数关系式是（）

A、 $y = - \frac{1}{4} x^{2} + x$ B、 $y = - x^{2} + x$ C、 $y = - \frac{1}{4} x^{2} - x$ D、 $y = - x^{2} - x$

查看试题解析

二、填空题

8. 如果函数 $y = (m - 3) x^{| m - 1 |} + 3 x - 1$ 是二次函数，那么 $m$ 的值为．

查看试题解析
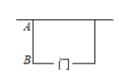
9. 如图，用长为16m的篱笆，一面利用墙（墙足够长）围成一块留有一扇1m宽的门的长方形花圃．设花圃的宽AB为xm，面积为ym² ，则y与x的函数表达式为．

查看试题解析
10. 如图①是一座石拱桥，它是一个横断面为抛物线形状的拱桥，若桥拱的最大高度为16米，跨度为40米，图②为它在坐标系中的示意图，则抛物线的解析式是（写出顶点式和一般式均可）．

查看试题解析
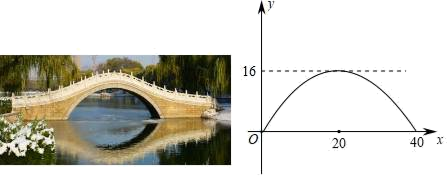11. 二次函数的解析式为 $y = m x^{m^{2} - 3 m + 2}$ ，则常数m的值为．

查看试题解析
12. 矩形周长等于40，设矩形的一边长为 $x$ ，那么矩形面积 $S$ 与边长 $x$ 之间的函数关系式为.

查看试题解析

三、解答题

13.
如图，扇形OAB的半径为4，圆心角∠AOB=90°，点C是上异于点A、B的一动点，过点C作CD⊥OB于点D，作CE⊥OA于点E，联结DE，过O点作OF⊥DE于点F，点M为线段OD上一动点，联结MF，过点F作NF⊥MF，交OA于点N．
（1）当tan $∠$ MOF= $\frac{1}{3}$ 时，求 $\frac{O M}{N E}$ 的值；
（2）设OM=x，ON=y，当 $\frac{O M}{O D} = \frac{1}{2}$ 时，求y关于x 的函数解析式，并写出它的定义域；
（3）在（2）的条件下，联结CF，当△ECF与△OFN相似时，求OD的长．

查看试题解析
14. 如图所示，已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为 $20 c m ， A C$ 与 $M N$ 在同一条直线上.开始时点 $A$ 与点 $N$ 重合，正方形 $M N P Q$ 不动， $△ A B C$ 以 $2 c m / s$ 的速度向左运动，最终点 $A$ 与点 $M$ 重合.

(1)、求重叠部分的面积 $y (c m^{2})$ 关于时间 $t (s)$ 的函数表达式和自变量的取值范围.

(2)、分别求当t=1，2时，重叠部分的面积..

查看试题解析

四、综合题

15. 如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，0)，A(12，0)，B(8，6)，C(0，6)．动点P从点O出发，以每秒3个单位长度的速度沿边向OA终点A运动；动点Q从点B同时出发，以每秒2个单位长度的速度沿边BC向终点C运动．设运动的时间为t秒，PQ $^{2}$ =y．

(1)、直接写出y关于t的函数解析式及t的取值范围：；

(2)、当PQ=3 $\sqrt{5}$ 时，求t的值；

(3)、连接OB交PQ于点D，若双曲线 $y = \frac{k}{x} (x \neq 0)$ 经过点D，问k的值是否变化？若不变化，请求出k的值；若变化，请说明理由．

查看试题解析
16.

(1)、基础巩固
如图1，已知正方形ABCD中，E是边4B的延长线上一点，过点C作CF⊥CE，交AD于点F。

求证：CE=CF。

(2)、尝试应用
如图2，已知正方形ABCD的边长为1，M是边4B所在直线上一点，N是边AD所在直线上一点，且∠MCN=45°。记AM=x，S_△MCN=y。请直接写出y与x之间的函数关系式。

(3)、应用拓广
如图12-3，已知菱形ABCD是一个菱长为6km的森林生态保护区，∠A=60°，沿保护区的边缘AB、AD已修建好道路AP和AQ，现要从保护区外新修建一条道路ECF，将道路AP、AQ连通．已知∠ECF=120°，求道路ECF的最短路程。

查看试题解析