湘教版数学八年级下册 2.7 正方形同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等2. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE , 其中正确结论有( )
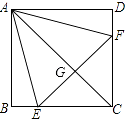 A、2个 B、3个 C、4个 D、5个3. 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A、2个 B、3个 C、4个 D、5个3. 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( ) A、 B、 C、 D、4. 如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,则下列四个判断中不一定正确的是( )
A、 B、 C、 D、4. 如图,在△ABC中,点D,E,F分别是AB,BC,AC的中点,则下列四个判断中不一定正确的是( )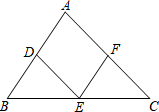 A、四边形ADEF一定是平行四边形 B、若∠B+∠C=90°,则四边形ADEF是矩形 C、若四边形ADEF是菱形,则△ABC是等边三角形 D、若四边形ADEF是正方形,则△ABC是等腰直角三角形5. 如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:
A、四边形ADEF一定是平行四边形 B、若∠B+∠C=90°,则四边形ADEF是矩形 C、若四边形ADEF是菱形,则△ABC是等边三角形 D、若四边形ADEF是正方形,则△ABC是等腰直角三角形5. 如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形 ②△AED≌△GED
③∠DFG=112.5° ④BC+FG=1.5
其中正确的结论是( )
 A、①②③④ B、①②③ C、①② D、②6. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )
A、①②③④ B、①②③ C、①② D、②6. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )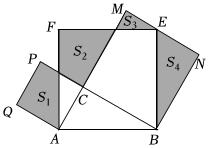 A、 B、 C、 D、7. 如图,正方形的边长为 , 点 , 分别在 , 上,若 , 且 , 则的长为( )
A、 B、 C、 D、7. 如图,正方形的边长为 , 点 , 分别在 , 上,若 , 且 , 则的长为( )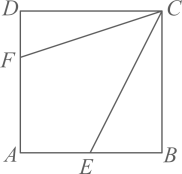 A、 B、 C、 D、8. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )
A、 B、 C、 D、8. 如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E , PF⊥CD于点F , 连接EF , 有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于 . 其中正确结论的个数是( )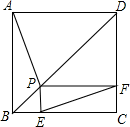 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 如图,两个边长为4的正方形重叠在一起,点是其中一个正方形的中心,则图中阴影部分的面积为 .
 10. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.
10. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.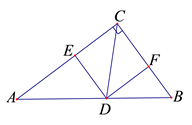 11. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.
11. 如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是.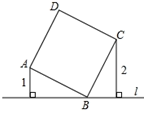 12. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 .
12. 如图,正方形的边长为 , 点 , 分别在 , 上若 , , 则的长为 . 13. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
13. 如图,在中, , 以的三边为边向外作正方形 , 正方形 , 正方形 , 连接 , , 作交于点P , 记正方形和正方形的面积分别为 , , 若 , , 则:等于 .
三、解答题
-
14. 如图,在中, , 过点的直线 , 为上一点,过点作 , 交直线于点 , 垂足为 , 连接 , .
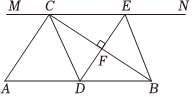 (1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.15. 已知正方形 .
(1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.15. 已知正方形 .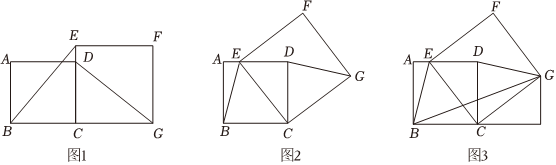 (1)、如图所示,若点在的延长线上,以为一边构造正方形 , 连接和 , 则与的数量关系为 , 位置关系为 .(2)、如图所示,若是边上的一个动点,以为一边在的右侧作正方形 , 连接和请判断线段与有怎样的数量关系和位置关系,并说明理由;(3)、如图所示,在(2)的条件下,连接若 , , 求线段的长.
(1)、如图所示,若点在的延长线上,以为一边构造正方形 , 连接和 , 则与的数量关系为 , 位置关系为 .(2)、如图所示,若是边上的一个动点,以为一边在的右侧作正方形 , 连接和请判断线段与有怎样的数量关系和位置关系,并说明理由;(3)、如图所示,在(2)的条件下,连接若 , , 求线段的长.四、综合题

