湘教版数学八年级下册 2.7 正方形同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 下列命题中,真命题是( )A、两条对角线垂直的四边形是菱形 B、对角线垂直且相等的四边形是正方形 C、两条对角线相等的四边形是矩形 D、两条对角线相等的平行四边形是矩形2. 如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
 A、1 B、 C、 D、3. 如图所示,是用4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
A、1 B、 C、 D、3. 如图所示,是用4个全等的直角三角形与1个正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) A、①②③ B、①②④ C、②③④ D、①②③④4. 如图,围绕在正方形四周的四条线段 , , , 中,长度最长的是( )
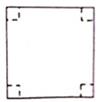
A、①②③ B、①②④ C、②③④ D、①②③④4. 如图,围绕在正方形四周的四条线段 , , , 中,长度最长的是( )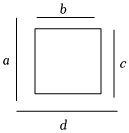 A、 B、 C、 D、5. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( )
A、 B、 C、 D、5. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( ) A、 B、 C、 D、6. 如图,在Rt中,是斜边BC的中点,连结AM,以AM为边作正方形AMEF.若 , 则( )
A、 B、 C、 D、6. 如图,在Rt中,是斜边BC的中点,连结AM,以AM为边作正方形AMEF.若 , 则( ) A、 B、 C、12 D、167. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( )
A、 B、 C、12 D、167. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( ) A、 B、 C、 D、8. 一个正方形和两个等边三角形的位置如图所示.若 , 则( )
A、 B、 C、 D、8. 一个正方形和两个等边三角形的位置如图所示.若 , 则( )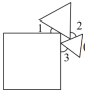 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,是正方形内的一点,连结、 , 将绕点逆时针旋转到的位置,则它旋转了 度.
 10. 如图,图中的三角形为直角三角形,已知正方形A和正方形B的面积分别为25和9,则正方形C的面积为 .
10. 如图,图中的三角形为直角三角形,已知正方形A和正方形B的面积分别为25和9,则正方形C的面积为 .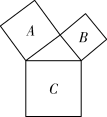 11. 小明在学习完四边形后,整理成如图所示的知识结构图,发现通过添加边、角或对角线等元素的特殊条件,就能得到特殊的四边形.写出条件①中你认为合适的边、角或对角线的条件是 . (写出一个即可)
11. 小明在学习完四边形后,整理成如图所示的知识结构图,发现通过添加边、角或对角线等元素的特殊条件,就能得到特殊的四边形.写出条件①中你认为合适的边、角或对角线的条件是 . (写出一个即可) 12. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .
12. 如图,在边长为2的正方形中,E,F分别是上的动点,M,N分别是的中点,则的最大值为 .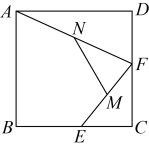 13. 如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=
13. 如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=
三、解答题
-
14. 如图,四边形ABCD是正方形,C是BC上任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.求证:DE-BF=EF.
 15. 如图①,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
15. 如图①,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F. (1)、如图②,取AB的中点H,连结HE,求证:AE=EF.(2)、如图③,若点E是BC的延长线上(除点C外)的任意一点,其他条件不变,结论“AE=EF"仍然成立吗?如果成立,写出证明过程;如果不成立,请说明理由.
(1)、如图②,取AB的中点H,连结HE,求证:AE=EF.(2)、如图③,若点E是BC的延长线上(除点C外)的任意一点,其他条件不变,结论“AE=EF"仍然成立吗?如果成立,写出证明过程;如果不成立,请说明理由.四、综合题