2023-2024学年湘教版初中数八年级下册 2.6.2 菱形的判定同步分层训练基础题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 下列命题中，为假命题的是（）

A、两组邻边分别相等的四边形是菱形 B、对角线互相垂直平分的四边形是菱形 C、四个角相等的四边形是矩形 D、对角线相等的平行四边形是矩形

查看试题解析
2. 如图，四边形ABCD的对角线AC、BD相交于点O，下列判断正确的是（）

A、若 $A C ⊥ B D$ ，则四边形ABCD是菱形 B、若 $A C = B D$ ，则四边形ABCD是矩形 C、若 $A C ⊥ B D$ ， $A C = B D$ ，则四边形ABCD是正方形 D、若 $A O = O C$ ， $B O = O D$ ，则四边形ABCD是平行四边形

查看试题解析
3. 下列说法正确的是（）

A、邻边相等的平行四边形是矩形 B、矩形的对角线互相平分 C、对角线互相垂直的四边形是菱形 D、一组对边相等，另一组对边平行的四边形是平行四边形

查看试题解析
4. 如图，用直尺和圆规作菱形 $A B C D$ ，作图过程如下：①作锐角 $∠ A$ ；②以点 $A$ 为圆心，以任意长度为半径作弧，与 $∠ A$ 的两边分别交于点 $B$ ， $D$ ；③分别以点 $B$ ， $D$ 为圆心，以 $A D$ 的长度为半径作弧，两弧相交于点 $C$ ，分别连接 $D C$ ， $B C$ ，则四边形 $A B C D$ 即为菱形，其依据是（）

A、一组邻边相等的四边形是菱形 B、四条边相等的四边形是菱形 C、对角线互相垂直的平行四边形是菱形 D、每条对角线平分一组对角的平行四边形是菱形

查看试题解析
5. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

查看试题解析
6. 如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO．若∠DAC＝28°，则∠OBC的度数为（　　）

A、28° B、52° C、62° D、72°

查看试题解析
7. 如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=12，AB=10，则AE的长为（　）

A、20 B、16 C、12 D、8

查看试题解析
8. 两张全等的矩形纸片 $A B C D$ ， $A E C F$ 按如图所示的方式交叉叠放， $A B = A F$ ， $A E = B C . A E$ 与 $B C$ 交于点 $G$ ， $A D$ 与 $C F$ 交于点 $H$ ，且 $∠ A G B = 30 °$ ， $A B = 2$ ，则四边形 $A G C H$ 的周长为（）

A、 $4$ B、 $8$ C、 $12$ D、 $16$

查看试题解析

二、填空题

9. 平行四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 互相垂直，那么这个四边形的邻边．（填“相等”或“不相等”）．

查看试题解析
10. 如图，请你添加一个适当的条件，使平行四边形ABCD成为菱形．

查看试题解析
11. 如图，在给定的一张平行四边形纸片上作一个菱形．小米的作法是：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．则小米的依据是．

查看试题解析
12. 如图， $∠ A B C = 30 °$ ， $A B = 4 \sqrt{3}$ ，点 $D$ 是射线 $B C$ 上的任意一点，连接 $A D$ ，以 $A D$ ， $B D$ 为邻边作平行四边形 $A D B E$ ，连 $D E$ ，则线段 $D E$ 的最小值为．

查看试题解析
13. 如图，在矩形 $A B C D$ 中，对角线 $A C$ 的垂直平分线分别交 $A B$ ， $C D$ 于点 $E$ ， $F$ ，连接 $A F$ ， $C E$ ，如果 $∠ B C E = 26 °$ ，则 $∠ C A F =$

查看试题解析

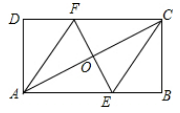
三、解答题

14. 如图，在四边形ABCD中，AB与CD不平行，E，F，G，H分别是AD，BC，BD，AC的中点．

(1)、求证：四边形EGFH是平行四边形．

(2)、①当AB与CD满足条件时，四边形EGFH是菱形，请说明理由；
②当AB与CD满足条件时，四边形EGFH是矩形，请说明理由．

查看试题解析
15. 如图，在矩形 $A B C D$ 中，点 $O$ 是对角线 $A C$ 的中点，过点 $O$ 作 $E F ⊥ A C$ 交 $B C$ 于点 $E$ ，交 $A D$ 于点 $F$ ，连接 $A E$ ， $C F$ ．

(1)、求证：四边形 $A E C F$ 是菱形；

(2)、若 $A F = 10$ ， $A C = 16$ ，求四边形 $A E C F$ 的面积．

查看试题解析

四、综合题

16. 如图：在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点O，过点A作 $A E ⊥ B C$ 于点E，延长 $B C$ 至点F，使 $C F = B E$ ，连接 $D F$ ．

(1)、求证：四边形 $A E F D$ 是矩形；

(2)、若 $B F = 16$ ， $D F = 8$ ，求 $C D$ 的长．

查看试题解析
17. 如图

如图 $1$ ， $A E / / B F$ ， $A B / / C D$ ， $B D$ 平分 $∠ A B C$ ．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、如图 $2$ ， $C D = 5$ ， $A C = 6$ ， $D M ⊥ B F$ 交 $B F$ 于点 $M$ ，已知点 $P$ 是 $B D$ 上一动点，连接 $P C$ ， $P M .$ 求 $△ P C M$ 周长的最小值．

查看试题解析