湘教版数学八年级下册 2.6.1 菱形的性质同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,菱形的周长为 , 对角线 , 交于点 , 为的中点,则的长等于( )
 A、 B、 C、 D、2. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线平分一组对角3. 已知菱形的对角线的长度恰为方程的两个实数根,则菱形的周长为( )A、12 B、16 C、20 D、244. 下列说法错误的是( )A、平行线间的距离处处相等 B、菱形的对角线相等 C、对角线互相平分的四边形边平行四边形 D、有三个角是直角的四边形是矩形5. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
A、 B、 C、 D、2. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线平分一组对角3. 已知菱形的对角线的长度恰为方程的两个实数根,则菱形的周长为( )A、12 B、16 C、20 D、244. 下列说法错误的是( )A、平行线间的距离处处相等 B、菱形的对角线相等 C、对角线互相平分的四边形边平行四边形 D、有三个角是直角的四边形是矩形5. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )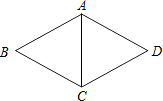 A、5 B、10 C、15 D、206. 如图,菱形ABCD中,∠D=140°,则∠1的大小是( )
A、5 B、10 C、15 D、206. 如图,菱形ABCD中,∠D=140°,则∠1的大小是( ) A、10° B、20° C、30° D、40°7. 在菱形ABCD中,∠ABC=60°,AB=1,E为BC边的中点则对角线BD上的动点P到E,C两点的距离之和的最小值为( ).
A、10° B、20° C、30° D、40°7. 在菱形ABCD中,∠ABC=60°,AB=1,E为BC边的中点则对角线BD上的动点P到E,C两点的距离之和的最小值为( ). A、 B、 C、 D、8. 如图,数学实践活动课上小明用两根木条钉成一个角形框架 , 且 , , 将一根橡皮筋两端固定在点A,B处,拉展成线段AB,在平面内,拉动橡皮筋上的一点 , 当四边形OACB是菱形时,橡皮筋再次被拉长了( )
A、 B、 C、 D、8. 如图,数学实践活动课上小明用两根木条钉成一个角形框架 , 且 , , 将一根橡皮筋两端固定在点A,B处,拉展成线段AB,在平面内,拉动橡皮筋上的一点 , 当四边形OACB是菱形时,橡皮筋再次被拉长了( )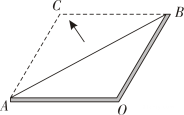 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 菱形的对角线长分别为 , , 则菱形的面积为 .10. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且 , , 于点E,则 .
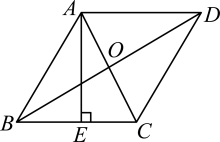 11. 如图,菱形的对角线 , 相交于点 , 点为边上一动点不与点 , 重合 , 于点 , 于点 , 若 , , 则的最小值为 .
11. 如图,菱形的对角线 , 相交于点 , 点为边上一动点不与点 , 重合 , 于点 , 于点 , 若 , , 则的最小值为 .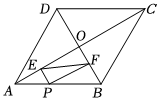 12. 如图,四边形是菱形, , 于点 , 则 .
12. 如图,四边形是菱形, , 于点 , 则 . 13. 如图,在菱形中,已知 , , 对角线、交于点 , 那么菱形的面积为 .
13. 如图,在菱形中,已知 , , 对角线、交于点 , 那么菱形的面积为 . 14. 如图,菱形的对角线 , 相交于点O , M , N分别是 , 边的中点,连接交于点P , 以下说法正确的是(填写序号即可).
14. 如图,菱形的对角线 , 相交于点O , M , N分别是 , 边的中点,连接交于点P , 以下说法正确的是(填写序号即可).① ② ③ ④

三、解答题
-
15. 如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF,求证:AE=AF.
 16. 如图①,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连结EF,FG,GH,HE,得到四边形EFGH(即四边形ABCD的中点四边形).
16. 如图①,四边形ABCD四条边上的中点分别为E,F,G,H,顺次连结EF,FG,GH,HE,得到四边形EFGH(即四边形ABCD的中点四边形). (1)、四边形EFGH的形状是 ▲ , 证明你的结论.(2)、如图②,连结四边形ABCD的对角线AC与BD,当AC与BD满足条件 ▲ 时,四边形EFGH是矩形,证明你的结论.(3)、你学过的哪种特殊四边形的中点四边形是矩形?说明理由.
(1)、四边形EFGH的形状是 ▲ , 证明你的结论.(2)、如图②,连结四边形ABCD的对角线AC与BD,当AC与BD满足条件 ▲ 时,四边形EFGH是矩形,证明你的结论.(3)、你学过的哪种特殊四边形的中点四边形是矩形?说明理由.四、综合题
-
17. 如图,矩形的顶点 , 分别在菱形的边 , 上,顶点 , 分别在菱形的对角线上.
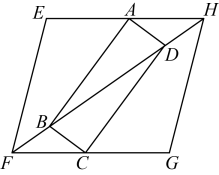 (1)、求证:;(2)、若为的中点,菱形的周长是28,求的长.18.
(1)、求证:;(2)、若为的中点,菱形的周长是28,求的长.18.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
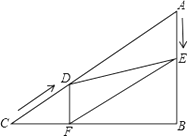 (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时,△DEF为直角三角形?请说明理由.