2023-2024学年湘教版初中数八年级下册 2.5.2 矩形的判定同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

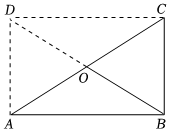
1. 如图，已知 $▱ A B C D$ 的四个内角的平分线分别交于点 $E$ 、 $F$ 、 $G$ 、 $H$ ，则四边形 $E F G H$ 的形状是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
2. 如图所示，在正方形 $A B C D$ 中， $P$ 是对角线 $B D$ 上一点，过 $P$ 作 $P E ⊥ B C$ ， $P F ⊥ D C$ ，垂足分别为 $E$ 、 $F$ ，连接 $E F$ ，若 $E F = 5$ ，则 $A P$ 的长为（）

A、 $5$ B、 $4$ C、 $\sqrt{5}$ D、 $\sqrt{7}$

查看试题解析
3. 在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $O$ 是 $A C$ 的中点，求证： $B O = \frac{1}{2} A C$ ．
证明：如图，延长 $B O$ 至点 $D$ ，使 $O D = B O$ ，连接 $A D$ ， $C D$ ．
……
$∴ A C = B D = 2 O B$ ，
$∴ B O = \frac{1}{2} A C$ ．
下面是“……”部分被打乱顺序的证明过程：①∴四边形 $A B C D$ 是平行四边形；②∵ $∠ A B C = 90 °$ ；③∵ $O A = O C$ ， $O B = O D$ ；④∴四边形 $A B C D$ 是矩形．

A、③①②④ B、③②①④ C、②③①④ D、②①③④

查看试题解析
4. 如图，矩形ABCD中， $A B = 6 ， A D = 8$ ，且有一点P从B点沿着BD往D点移动，若过P点作AB的垂线交AB于E点，过P点作AD的垂线交AD于F点，则EF的长度最小为多少（）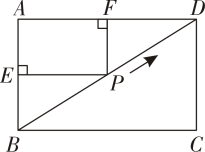

A、 $\frac{14}{5}$ B、 $\frac{24}{5}$ C、5 D、7

查看试题解析
5. 下列命题中错误的是（）

A、矩形的对角线相等 B、对角线相等的四边形是矩形
C、两组对边分别相等的四边形是平行四边形 D、平行四边形的对边相等

查看试题解析
6. 如图，在四边形 $A B C D$ 中， $E$ ， $F$ ， $G$ ， $H$ 分别是边 $A B$ ， $B C$ ， $C D$ ， $D A$ 的中点 $.$ 要使四边形 $E F G H$ 为矩形，可以添加的一个条件是（）

A、四边形 $A B C D$ 是矩形 B、 $A C$ 、 $B D$ 互相平分 C、 $A C = B D$ D、 $A C ⊥ B D$

查看试题解析
7. 如图，在矩形 $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $O$ ，点 $P$ 为边 $A D$ 上一点，过 $P$ 分别作 $P E ⊥ A C$ ， $P F ⊥ B D$ ，垂足为点 $E$ ， $F$ ，过 $A$ 作 $A H ⊥ B D$ ，垂足为 $H$ ．若知道 $△ A P E$ 与 $△ D P F$ 的周长和，则一定能求出（）

A、 $△ B O C$ 的周长 B、 $△ A D H$ 的周长 C、 $△ A B C$ 的周长 D、四边形 $A P F H$ 的周长

查看试题解析
8. 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥ CD于点F，连接EF，给出下列五个结论：① AP＝EF；② AP⊥ EF；③∠PFE＝∠BAP；④ PD＝EC；⑤ PB²+PD²＝2PA² ，正确结论是（　　）

A、① ③ B、① ② ③ C、① ③ ⑤ D、① ② ③ ⑤

查看试题解析

二、填空题

9. 如图，AC平分∠BAD，AB∥CD， BC=4， ∠BAD＝30°，∠B＝90° ，则CD的长为．

查看试题解析
10. 如图，矩形 $A B C D$ 中， $A B = 6$ ， $A D = 4$ ， $E$ 是 $A B$ 的中点， $F$ 是线段 $E C$ 上一动点， $P$ 为 $D F$ 的中点，连接 $P B$ ，则线段 $P B$ 的最小值为．

查看试题解析
11. 如图，在Rt $△ A B C$ 中， $∠ B A C = 9 0^{°} ， A B = 6 ， A C = 8 ， P$ 为边BC上一个动点 $(P$ 不与B、C重合），PE⊥AB于 $E ， P F ⊥ A C$ 于F，M为EF中点，则AM的最小值是.

查看试题解析
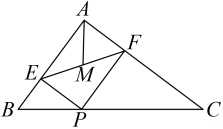12. 如图，长方形ABCD中，AB＝6，BC＝8，E为BC上一点，且BE＝2，F为AB边上的一个动点，连接EF ，将EF绕着点E顺时针旋转30°到EG的位置，连接FG和CG ，则CG的最小值为．

查看试题解析
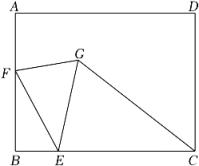13. 如图，点P是矩形 $A B C D$ 内任意一点，连结 $P A ， P B ， P C ， P D$ ，记 $∠ P A B = θ_{1} ， ∠ P B C = θ_{2} ， ∠ P C D = θ_{3} ， ∠ P D A = θ_{4}$ ，则下列各结论一定成立的有（填序号）
① $S_{△ P A D} + S_{△ P B C} = S_{△ P A B} + S_{△ P C D}$ ；②若 $∠ A P B = 80 ° ， ∠ D P C = 50 °$ ，则 $θ_{1} - θ_{2} + θ_{3} - θ_{4} = 50 °$ ；
③ $P A^{2} + P C^{2} = P B^{2} + P D^{2}$ ；④ $S_{△ A B P} = S_{△ A D P}$ ，则P在对角线 $A C$ 上

查看试题解析

三、解答题

14. 如图所示， $△ A B C$ 中， $D$ 是 $B C$ 中点， $E$ 是 $A D$ 的中点，过点 $A$ 作 $B C$ 的平行线交 $C E$ 的延长线于 $F$ ，连接 $B F$ ．

(1)、判断并证明四边形 $A F B D$ 的形状；

(2)、当 $△ A B C$ 满足什么条件时，四边形 $A F B D$ 是矩形，证明你的结论．

查看试题解析
15. 如图 $1$ ，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 120 °$ ，点 $D$ 是边 $A B$ 上一动点，将线段 $C D$ 绕点 $C$ 逆时针旋转 $120 °$ 得到 $C E$ ，连接 $B E$ ．

(1)、求 $∠ C B E$ 的度数；

(2)、连接 $A E$ ，若 $A D = 4$ ， $∠ A C D = 30 °$ ，求线段 $A E$ 的长；

(3)、如图 $2$ ，若 $A D = A C$ ， $B D = 2$ ，点 $M$ 为 $C D$ 中点， $A M$ 的延长线与 $B C$ 交于点 $P$ ，与 $B E$ 交于点 $N$ ，求线段 $B N$ 的长．

查看试题解析

四、综合题

16. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．

(1)、求证：四边形ADFE是矩形；

(2)、连接OF，若AD＝6，EC＝4，∠ABF＝60°，求OF的长度．

查看试题解析
17. 在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

(1)、在图1中证明CE=CF；

(2)、若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

(3)、若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．

查看试题解析