湘教版数学八年级下册 2.5.1 矩形的性质同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
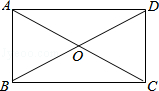 A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB2. 如图,在矩形中,分别是上的点,分别是的中点. , , 则线段的长为( )
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB2. 如图,在矩形中,分别是上的点,分别是的中点. , , 则线段的长为( ) A、6 B、6.5 C、7 D、53. 一个长方形,面积为 . 一边长为 . 那么这条边的邻边长为( )A、 B、 C、 D、4. 如图,在矩形中,对角线、相交于点 , 平分交边于点 , 点是的中点,连接 , 若 , , 则的长度为( )
A、6 B、6.5 C、7 D、53. 一个长方形,面积为 . 一边长为 . 那么这条边的邻边长为( )A、 B、 C、 D、4. 如图,在矩形中,对角线、相交于点 , 平分交边于点 , 点是的中点,连接 , 若 , , 则的长度为( ) A、 B、 C、 D、5. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为.若 , 则( )
A、 B、 C、 D、5. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为.若 , 则( ) A、20° B、30° C、40° D、50°6. 如图,把长方形纸片沿对角线折叠,设重叠部分为 , 下列说法错误的是( )
A、20° B、30° C、40° D、50°6. 如图,把长方形纸片沿对角线折叠,设重叠部分为 , 下列说法错误的是( ) A、 B、 C、 D、7. 如图,把长方形 沿EF对折,若 ,则 的度数为( )
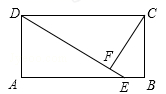
A、 B、 C、 D、7. 如图,把长方形 沿EF对折,若 ,则 的度数为( ) A、 B、 C、 D、8. 如图,在矩形ABCD中, , , 点E是边CD上一点,连接AE , 矩形ABCD沿AE折叠,点D的对应点恰好落在BC上的点F处.则AE的长为( )
A、 B、 C、 D、8. 如图,在矩形ABCD中, , , 点E是边CD上一点,连接AE , 矩形ABCD沿AE折叠,点D的对应点恰好落在BC上的点F处.则AE的长为( ) A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
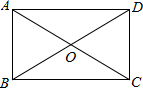
9. 如图,在矩形中,对角线和交于点O , 若 , 则 .
 10. 已知黄金矩形的宽为﹣2,则这个黄金矩形的面积是 . (注:宽∶长=的矩形为黄金矩形)11. 如图,在矩形纸片中, , , 将矩形纸片折叠,使点B与点D重合,那么的周长是cm.
10. 已知黄金矩形的宽为﹣2,则这个黄金矩形的面积是 . (注:宽∶长=的矩形为黄金矩形)11. 如图,在矩形纸片中, , , 将矩形纸片折叠,使点B与点D重合,那么的周长是cm.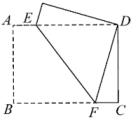 12. 矩形ABCD中,M为对角线BD的中点,点N在边AD上,且 . 当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .13. 如图,在平面直角坐标系中,矩形的两边 , 分别在轴和轴上,并且 , .若把矩形绕着点逆时针旋转,使点恰好落在边上的处,则点的坐标为.
12. 矩形ABCD中,M为对角线BD的中点,点N在边AD上,且 . 当以点D,M,N为顶点的三角形是直角三角形时,AD的长为 .13. 如图,在平面直角坐标系中,矩形的两边 , 分别在轴和轴上,并且 , .若把矩形绕着点逆时针旋转,使点恰好落在边上的处,则点的坐标为.
三、解答题
-
14. 如图,在矩形ABCD中,AD=4,AB=10,P是AB上一动点,M,N,E分别是PD,PC,CD的中点.
 (1)、求证:四边形PMEN是平行四边形.(2)、四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.15. 如图,长方形ABCD中,点E是AD的中点,将△ABE沿BE向下折叠后得到△GBE,将BG延长线交直线 DC于点F.
(1)、求证:四边形PMEN是平行四边形.(2)、四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.15. 如图,长方形ABCD中,点E是AD的中点,将△ABE沿BE向下折叠后得到△GBE,将BG延长线交直线 DC于点F. (1)、若点G恰好落在边BC上,则AD与AB的数量关系是.(2)、如果点G在长方形ABCD的内部,如图所示.
(1)、若点G恰好落在边BC上,则AD与AB的数量关系是.(2)、如果点G在长方形ABCD的内部,如图所示.①试探究线段BF,AB,DF之间的数量关系,并说明理由;
②若DF=DC,AD=8,求AB的长度.
四、综合题