2023-2024学年湘教版初中数八年级下册 2.2.2 平行四边形的判定同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在四边形ABCD中，对角线AC、BD相交于点O．下列条件不能判定四边形ABCD为平行四边形的是（　　）

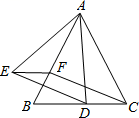
A、AB∥CD，AD∥BC B、OA＝OC，OB＝OD C、AB＝CD，AD＝BC D、AB∥CD，AD＝BC

查看试题解析
2. 如图，在▱ $A B C D$ 中，已知 $A D = 8 c m$ ， $A B = 5 c m$ ， $D E$ 平分 $∠ A D C$ 交 $B C$ 边于点 $E$ ，则 $B E$ 等于（）

A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $4 c m$

查看试题解析
3. 如图，点 $C$ 是线段 $A B$ 上的动点 $($ 不与点 $A$ 、 $B$ 重合 $)$ ，分别以 $A C$ 、 $B C$ 为边向上作等边三角形 $△ A C D$ 和 $△ B C E$ ，延长 $A D$ 、 $B E$ 交于点 $F$ ，若 $A B = 4$ ，则四边形 $C E F D$ 的周长是（）

A、 $4$ B、 $8$ C、 $10$ D、 $12$

查看试题解析
4. 如图，在四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，下列条件中不能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A D = B C$ ， $A B = C D$ B、 $A B ∥ C D$ ， $A D ∥ B C$ C、 $A D ∥ B C$ ， $A B = D C$ D、 $O A = O C$ ， $A D ∥ B C$

查看试题解析
5. 如图，已知△ABC是边长为3的等边三角形，点D是边BC上的一点，且BD＝1，以AD为边作等边△ADE，过点E作EF∥BC，交AC于点F，连接BF，则下列结论中①△ABD≌△BCF；②四边形BDEF是平行四边形；③S_四边形_BDEF $= \frac{\sqrt{3}}{2}$ ；④S_△_AEF $= \sqrt{3}$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图所示，在四边形 $A B C D$ 中， $A D / / B C$ ，要使四边形 $A B C D$ 成为平行四边形还需要条件（）

A、 $A B = D C$ B、 $∠ D = ∠ B$ C、 $A B = A D$ D、 $∠ 1 = ∠ 2$

查看试题解析
7. 如图，在△ABC中， $A B = 3$ ， $A C = 4$ ， $B C = 5$ ， △ABD ， △ACE ， △BCF都是等边三角形，下列结论中：① $A B ⊥ A C$ ；②四边形AEFD是平行四边形；③ $∠ D F E = 150 °$ ；④ $S_{四边形 A E F D} = 6$ ．正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图， $E$ 是 $▱ A B C D$ 的边 $A B$ 上的点， $Q$ 是 $C E$ 中点，连接 $B Q$ 并延长交 $C D$ 于点 $F$ ，连接 $A F$ 与 $D E$ 相交于点 $P$ ，若 $S_{△ A P D} = 3 c m^{2}$ ， $S_{△ B Q C} = 7 c m^{2}$ ，则阴影部分的面积为（） $c m^{2}$

A、24 B、17 C、13 D、10

查看试题解析

二、填空题

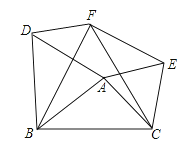
9.
如图，在△ABC中，AB=4，AC=3，BC=5，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积为

查看试题解析
10. 一艘船从 $O$ 处出发，沿南偏东 $55 °$ 方向行驶至 $A$ ，然后向正东方向行驶至 $C$ 后又改变航向，朝与出发时相反的方向行驶至 $B$ ，则 $∠ A C B$ 的度数为．

查看试题解析
11. 如图，河的两岸有 $A$ ， $B$ 两个水文观测点，为方便联络，要在河上修一座木桥 $M N ($ 河的两岸互相平行， $M N$ 垂直于河岸 $)$ ，现测得 $A$ ， $B$ 两点到河岸的距离分别是 $5$ 米， $4$ 米，河宽 $3$ 米，且 $A$ ， $B$ 两点之间的水平距离为 $12$ 米，则 $A M + M N + N B$ 的最小值是米 $.$

查看试题解析
12. 如图，△ABC为等腰直角三角形，∠ABC=90°，点P在AC的延长线上，且AC=CP=4，将△ABC沿AB方向平移得到△A'B'C'，连结PA'，PC'，则△PA'C'的周长的最小值为.

查看试题解析
13. 如图，在 $▱ A B C D$ 中，点E ， F分别是 $A D$ ， $B C$ 边的中点，延长 $C D$ 至点 $G$ ，使 $D G = C D$ ，以 $D G$ ， $D E$ 为边向 $▱ A B C D$ 外构造 $▱ D G M E$ ，连接 $B M$ 交 $A D$ 于点 $N$ ，连接 $F N$ ．若 $D G = D E = 2$ ， $∠ A D C = 60 °$ ，则 $F N$ 的长为．

查看试题解析

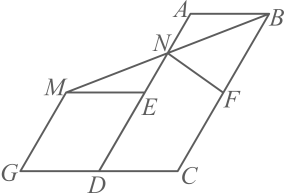
三、解答题

14. 在等边△ABC中，D为AC中点，延长BC至点E ，使CE＝DC ，连接ED并延长交AB于点F ．

(1)、求证：△DBE是等腰三角形；

(2)、DF与DE有怎样的数量关系？请说明理由．

查看试题解析
15. 如图，在 $▱ A B C D$ 中，点E在 $A B$ 上，点F在 $C D$ 上，且 $A E = C F$ ．

(1)、求证：四边形 $D E B F$ 是平行四边形；

(2)、若 $D E$ 为 $∠ A D C$ 的平分线，且 $A D = 3$ ， $E B = 2$ ，求 $▱ A B C D$ 的周长．

查看试题解析

四、综合题

16. 如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB＝60°，DC＝EF.

(1)、求证：四边形EFCD是平行四边形；

(2)、若BF＝EF，求证：AE＝AD.

查看试题解析
17. 如图
如图 $1$ ，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ A = ∠ C$ ．

(1)、求证： $A B ∥ D C$ ；

(2)、如图 $2$ ，点 $E$ 在线段 $A D$ 上，点 $G$ 在线段 $A D$ 的延长线上，连接 $B G$ ， $∠ A E B = 2 ∠ G$ ，求证： $B G$ 是 $∠ E B C$ 的平分线；

(3)、如图 $3$ ，在 $(2)$ 的条件下，点 $E$ 在线段 $A D$ 的延长线上， $∠ E D C$ 的平分线 $D H$ 交 $B G$ 于点 $H$ ，若 $∠ A B E = 66 °$ ，求 $∠ B H D$ 的度数 $. ($ 提示：需添加辅助线求解 $)$

查看试题解析