湘教版数学八年级下册 2.2.2 平行四边形的判定同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,在一束平行光线中插入一张对边平行的纸板,如果光线与纸板左上方所成的是 , 那么光线与纸板右下方所成的的度数为( )
 A、 B、 C、 D、2. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( )
A、 B、 C、 D、2. 在中,点D,E分别是 , 上的点,且 , 点F是延长线上一点,连接 . 添加下列条件后,不能判断四边形是平行四边形的是( ) A、 B、 C、 D、3. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A、 B、 C、 D、3. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )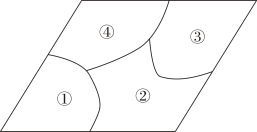 A、 B、 C、 D、4. 如图是嘉淇不完整的推理过程.
A、 B、 C、 D、4. 如图是嘉淇不完整的推理过程.
 A、 B、 C、 D、5. 下列图形中,一定可以拼成平行四边形的是( )
A、 B、 C、 D、5. 下列图形中,一定可以拼成平行四边形的是( )
A、两个等腰三角形 B、两个直角三角形 C、两个锐角三角形 D、两个全等三角形6. 如图,在四边形中, , 以点为圆心,以任意长为半径作弧,分别交 , 于点 , , 分别以 , 为圆心,以大于长为半径作弧,两弧在内交于点 , 作射线 , 交于点 , 交的延长线于点若 , , 则的长为( )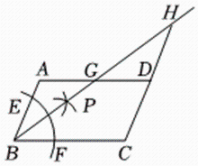 A、 B、 C、 D、7. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
A、 B、 C、 D、7. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
证法:如图,在▱中, , ,
.
又 ,
≌ ,
,
,
即 , .

证法:如图,连接交于点 , 连接 , .
在▱中, , .
又 ,
, 即 .
四边形是平行四边形,
.

下列说法错误的是( )
A、证法中证明三角形全等的直接依据是 B、证法中用到了平行四边形的对角线互相平分 C、证法和证法都用到了平行四边形的判定 D、证法和证法都用到了平行四边形的性质8. 如图,四边形是平行四边形,连接 , , 与的延长线交于点E , 连接交于F , 连接 , 下列结论中:①四边形是平行四边形;②;③若 , 则;④.正确的结论个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
9. 在四边形ABCD中,已知∠A+∠B=180°,要使四边形ABCD是平行四边形,还需添加一个条件,这个条件可以是 . (只需填写一种情况)
 10. 如图, , 过点的直线分别交于点 . 下列结论:
10. 如图, , 过点的直线分别交于点 . 下列结论: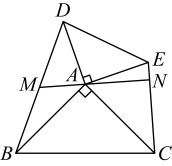
①若为的中点,则;
②若于点 , 则为的中点;
③若为的中点,则;
④ .
其中正确的结论有 . (填写序号即可)
11. 已知四边形 ,点 是对角线 与 的交点,且 ,请再添加一个条件,使得四边形 成为平行四边形,那么添加的条件可以是 . (用数学符号语言表达)12. 如图是小明和小颖玩跷跷板时的示意图,点是跷跷板的中点,支柱与地面垂直,且的长度为 , 若小明到水平线的距离为时小颖到地面的距离为 . 13.
13.如图,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个可使四边形ABCD是平行四边形,则你选的两个条件是 .(填写一组序号即可)

三、解答题
-
14. 如图,在四边形中, , , , ,
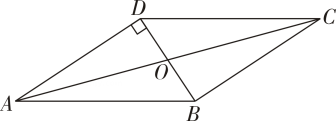 (1)、求证;四边形为平行四边形;
(1)、求证;四边形为平行四边形;
(2)、求四边形的面积.15. 如图,在▱ABCD中,点E在AB上,点F在CD上,AE=CF.求证:BF∥DE.
四、综合题

