湘教版数学八年级下册 2.2.1平行四边形的性质同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,在▱中, , 则( )
 A、 B、 C、 D、2. 如图所示,▱ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,▱ABCD的周长( )
A、 B、 C、 D、2. 如图所示,▱ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5,▱ABCD的周长( )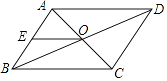 A、11 B、13 C、16 D、223. 如图,在平行四边形中,对角线 , 分别以点为圆心,以大于的长为半径画弧,两弧相交于点和点 , 作直线 , 交对角线于点 , 连接恰好垂直于边 , 若 , 则的长是( )
A、11 B、13 C、16 D、223. 如图,在平行四边形中,对角线 , 分别以点为圆心,以大于的长为半径画弧,两弧相交于点和点 , 作直线 , 交对角线于点 , 连接恰好垂直于边 , 若 , 则的长是( )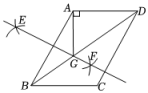 A、6 B、8 C、1 D、14. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作AF⊥BE,垂足为点F,若AF=5,BE=24,则CD的长为( )
A、6 B、8 C、1 D、14. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,过点A作AF⊥BE,垂足为点F,若AF=5,BE=24,则CD的长为( ) A、8 B、13 C、16 D、185.
A、8 B、13 C、16 D、185.如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长( )
 A、1 B、1.5 C、2 D、36. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )
A、1 B、1.5 C、2 D、36. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )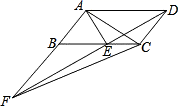 A、1个 B、2个 C、3个 D、4个7. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )
A、1个 B、2个 C、3个 D、4个7. 如图,在平行四边形中, , 点H、G分别是边上的动点.连接 , 点E为的中点,点F为的中点,连接 . 则的最大值与最小值的差为( )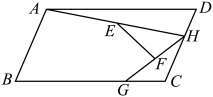 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
8. 如图,为平行四边形的对角线, , 点在上,连接 , 分别延长 , 交于点 , 若 , 则的长为 .
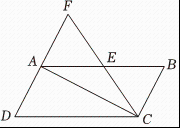 9. 如图,中,对角线、相交于点O,交于点E,已知的周长为12,则的周长为 .
9. 如图,中,对角线、相交于点O,交于点E,已知的周长为12,则的周长为 . 10. 如图,▱的对角线、相交于点 , 若 , 则▱的面积为 .
10. 如图,▱的对角线、相交于点 , 若 , 则▱的面积为 . 11. 在中, , , , 为外的一点,且 . 若点到边上的最短距离记为 , 当绕旋转时,的取值范围是 .
11. 在中, , , , 为外的一点,且 . 若点到边上的最短距离记为 , 当绕旋转时,的取值范围是 . 12. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .
12. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .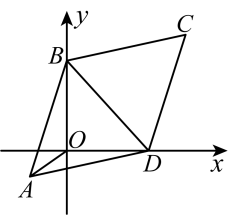
三、解答题
-
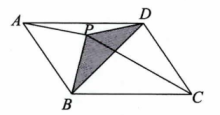
13. 已知平行四边形ABCD内有一点P,S△PAB=4,S△PBC=6,计算图中阴影部分△PBD的面积(要求写出过程)
 14.
14.如图1,已知▱ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是▱ABCD边上的一个动点.

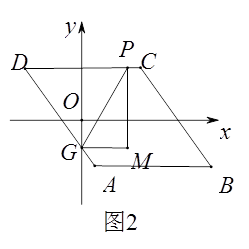 (1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
(1)、若点P在边BC上,PD=CD,求点P的坐标.(2)、若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)、若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).四、综合题

