湘教版数学八年级下册 2.1 多边形同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 下列多边形中,内角和等于的是( )A、
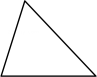 B、
B、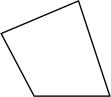 C、
C、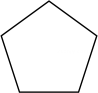 D、
D、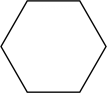 2. 若一个多边形的内角和等于其外角和的4倍,则这个多边形的边数为( )A、7 B、8 C、9 D、103. 六边形的内角和是( )A、540° B、720° C、900° D、360°4. 下列命题不正确的是( )A、从n边形的一个顶点出发,可以作条对角线 B、两个全等三角形对应边上的高相等 C、若两个三角形全等,则它们一定关于某条直线成轴对称 D、有两个内角分别为与的三角形是等腰三角形5. 图中x的值是( )
2. 若一个多边形的内角和等于其外角和的4倍,则这个多边形的边数为( )A、7 B、8 C、9 D、103. 六边形的内角和是( )A、540° B、720° C、900° D、360°4. 下列命题不正确的是( )A、从n边形的一个顶点出发,可以作条对角线 B、两个全等三角形对应边上的高相等 C、若两个三角形全等,则它们一定关于某条直线成轴对称 D、有两个内角分别为与的三角形是等腰三角形5. 图中x的值是( ) A、60 B、50 C、48 D、306. 下列说法中:①三角形三边高线的交点一定在三角形内部;②八边形有20条对角线;③两个连续偶数的平方差一定是8的倍数;④无论x取何值,代数式的值一定是正数.正确的有( )A、②④ B、①② C、①③ D、③④7. 如图a∥b,与相交,与相交,下列说法:
A、60 B、50 C、48 D、306. 下列说法中:①三角形三边高线的交点一定在三角形内部;②八边形有20条对角线;③两个连续偶数的平方差一定是8的倍数;④无论x取何值,代数式的值一定是正数.正确的有( )A、②④ B、①② C、①③ D、③④7. 如图a∥b,与相交,与相交,下列说法:①若 , 则;
②若 , 则c∥d;
③;
④ ,
正确的有( )
 A、①③④ B、①②③ C、①②④ D、②③8. 如图,∠ABC、∠ACD的平分线BP、CP交于点P,PF⊥BD,PG⊥BE,垂足分别为F、G,下列结论:①:=AB:BC;②∠APB+∠ACP=90°;③∠ABC+2∠APC=180°,其中正确的结论有( )
A、①③④ B、①②③ C、①②④ D、②③8. 如图,∠ABC、∠ACD的平分线BP、CP交于点P,PF⊥BD,PG⊥BE,垂足分别为F、G,下列结论:①:=AB:BC;②∠APB+∠ACP=90°;③∠ABC+2∠APC=180°,其中正确的结论有( ) A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
9. 若一个多边形的外角和比这个多边形的内角和小540°,则这个多边形的边数为.10. 如图①是阳泉市城区平坦垴汉代古井遗址,该井为平面九边形的木构支护结构,井壁四周由两端加工成原始榫卯结构的柏木相互搭接成闭合的正九边形后,逐层垒砌.如图②是该古井的平面示意图,则 .
 11. 如图,在一个三角形的纸片()中, , 则图中的度数为 .
11. 如图,在一个三角形的纸片()中, , 则图中的度数为 .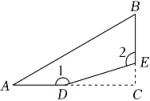 12. 如图,在四边形中, , 在边上分别找一点E、F,使周长最小,此时 .
12. 如图,在四边形中, , 在边上分别找一点E、F,使周长最小,此时 . 13. 如图由内角分别相等的四边形、五边形、六边形组合而成的图形中, , 则的度数为度.
13. 如图由内角分别相等的四边形、五边形、六边形组合而成的图形中, , 则的度数为度.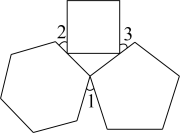
三、解答题
-
14. 如图,一个三角形的纸片ABC , 其中∠A=∠C .

①把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕.说明BC//DF;
②把△ABC纸片沿DE折叠,当点A落在四边形BCED内时(如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
③当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是 . (直接写出结论)
15. 探究归纳题: (1)、试验分析:
(1)、试验分析:如图1,经过A点可以作条对角线;同样,经过B点可以作条;经过C点可以作条;经过D点可以作条对角线.
通过以上分析和总结,图1共有条对角线.
(2)、拓展延伸:运用(1)的分析方法,可得:
图2共有条对角线;
图3共有条对角线;
(3)、探索归纳:对于n边形(n>3),共有条对角线.(用含n的式子表示)
(4)、特例验证:十边形有条对角线.
四、综合题

