2023-2024学年湘教版初中数八年级下册 2.1 多边形同步分层训练基础题
试卷更新日期：2024-01-27 类型：同步测试
一、选择题
-
1. 一个多边形的内角和为900°，则这个多边形是（ ）A、七边形 B、八边形 C、九边形 D、十边形2. 一个多边形的每个外角都是 ， 则这个多边形的边数为（ ）A、4 B、5 C、6 D、83. 正十二边形的外角为（ ）A、 B、 C、 D、4. 如图，小林从P点向西直走12m后，向左转，转动的角度为α，再走12m，如此重复，小林共走了108m回到点P，则α=（ ）
A、40o B、50 o C、80o D、不存在5. 如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）A、6 B、7 C、8 D、96. 如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=67°，则∠AED的度数是（ ）
A、78° B、88° C、92° D、112°7. 如图，小明从点A出发沿直线前进10米到达点B，向左转45%后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D……照这样走下去，小明第一次回到出发点A时所走的路程为（ ）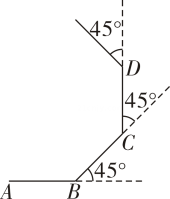
A、100米 B、80米 C、60米 D、40米8. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（ ）A、108° B、90° C、72° D、60°二、填空题
-
9. 正五边形的每个外角是度.10. 小林从P点向西直走8米后，向左转，转动的角度为α，再走8米，如此重复，小林共走了72米回到点P，则α为 ．11. 如图，在五边形ABCDE中，∠1+∠2+∠3+∠4+∠5=°.
12. 如图，∠1是六边形ABCDEF 的一个外角．若∠1=70°，则∠A+∠B+∠C+∠D+ ∠E的度数为.
13. 如图，△ABC中，∠A＝80°，剪去∠A后，得到四边形BCDE，则∠1＋∠2＝。
三、解答题
-
14. 一个多边形中，每个内角都相等，并且每个外角都等于它的相邻内角的(1)、求这个多边形的边数；(2)、求这个多边形的内角和．15. 如图，在四边形ABCD中，∠D=90° ，E是BC边上一点，EF⊥AE，交CD于点F．
(1)、若∠EAD= 60°，求∠DFE的度数；(2)、若CAEB=∠CEF，AE平分∠BAD，求证：∠B=∠C．四、综合题
