湘教版数学八年级下册 1.4 角平分线的性质同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,在中,和分别是 , 的平分线, , 与交于点 , 若 , , 则的长为( )
 A、4 B、 C、3 D、2. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=3,则两平行线AD与BC间的距离为( )
A、4 B、 C、3 D、2. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E.若PE=3,则两平行线AD与BC间的距离为( )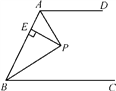 A、3 B、4 C、5 D、63. 如图,在中,平分 , , 垂足为 . 若 , , , 则的面积为( )
A、3 B、4 C、5 D、63. 如图,在中,平分 , , 垂足为 . 若 , , , 则的面积为( ) A、 B、3 C、5 D、64. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )
A、 B、3 C、5 D、64. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )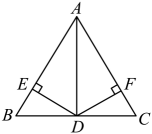 A、①④ B、②④ C、②③④ D、①②③④5. 如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( )
A、①④ B、②④ C、②③④ D、①②③④5. 如图,在Rt△ABC中,∠B=90°,以点A为圆心,适当长为半径画弧,分别交AB、AC于点D,E,再分别以点D、E为圆心,大于DE为半径画弧,两弧交于点F,作射线AF交边BC于点G,若BG=1,AC=4,则△ACG的面积是( ) A、1 B、 C、2 D、6. 如图,在中, , , 、是的两条角平分线, , 是上的一个动点,则线段最小值的是( )
A、1 B、 C、2 D、6. 如图,在中, , , 、是的两条角平分线, , 是上的一个动点,则线段最小值的是( ) A、3 B、4 C、5 D、67. 如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( )
A、3 B、4 C、5 D、67. 如图所示,在△ABC中,点O是∠BCA与∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,则点O到边BC的距离OD是( ) A、1 B、2 C、3 D、48. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )
A、1 B、2 C、3 D、48. 如图,在中,的垂直平分线与的外角平分线交于点D , 于点E , 交的延长线于点F , 则下列结论:①;②;③;④若 , , 则 , 其中一定成立的有( )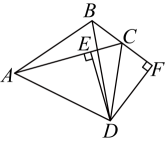 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
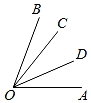
9. 如图,∠AOB=75°,∠BOC=15°,OD是∠AOC的平分线,则∠BOD的度数为 .
 10. 如图,在中, , CD是的平分线,于点E , .则的面积为.
10. 如图,在中, , CD是的平分线,于点E , .则的面积为.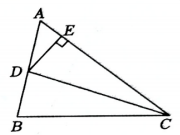 11. 如图,为的角平分线,且 , 为延长线上一点, .
11. 如图,为的角平分线,且 , 为延长线上一点, .
⑴若 , 则的度数是 .
⑵若 , , 则 , 之间的数量关系是 .
12. 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,下列结论:①∠DIF=45°;②CF
+BE=BC;③若AB=3,AC=4,则.其中正确的是 . 13. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .
13. 如图,在中, , , , , 是的平分线.若 , 分别是和上的动点,则的最小值是 .
三、解答题
-
14. 点为直线上一点,过点作射线 , 使 , 将一直角三角板的直角顶点放在点处.
 (1)、如图1,将三角板的一边与射线重合时,则;(2)、如图2,将三角板绕点逆时针旋转一定角度,此时是的角平分线,求旋转角的度数和的度数;(3)、将三角板绕点逆时针旋转过程中,当时,直接写出的度数.15. 如图1,点、分别在射线、上运动(不与点重合),、分别是和的角平分线,延长线交于点 .
(1)、如图1,将三角板的一边与射线重合时,则;(2)、如图2,将三角板绕点逆时针旋转一定角度,此时是的角平分线,求旋转角的度数和的度数;(3)、将三角板绕点逆时针旋转过程中,当时,直接写出的度数.15. 如图1,点、分别在射线、上运动(不与点重合),、分别是和的角平分线,延长线交于点 . (1)、若 , 则(直接写出答案)(2)、若 , 求出的度数(用含的代数式表示并写出理由)(3)、如图2,若 , 过点作交于点 , 求与的数量关系.
(1)、若 , 则(直接写出答案)(2)、若 , 求出的度数(用含的代数式表示并写出理由)(3)、如图2,若 , 过点作交于点 , 求与的数量关系.四、综合题