湘教版数学八年级下册 1.4 角平分线的性质同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,是的角平分线,于点E , , , , 则的长是( )
 A、9 B、8 C、7 D、62. 已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M( )A、在AC边的高上 B、在AC边的中线上 C、在∠ABC的平分线上 D、在AC边的垂直平分线上3. 如图,在△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、9 B、8 C、7 D、62. 已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M( )A、在AC边的高上 B、在AC边的中线上 C、在∠ABC的平分线上 D、在AC边的垂直平分线上3. 如图,在△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )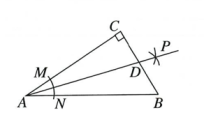 A、15 B、30 C、45 D、604. 如图,已知钝角三角形ABC,按以下步骤尺规作图,并保留作图痕迹.
A、15 B、30 C、45 D、604. 如图,已知钝角三角形ABC,按以下步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CB为半径画弧①;
步骤2:以A为圆心,AB为半径画弧②,交弧①于点D;
步骤3:连结BD,交AC的延长线于点E.
下列叙述正确的是( )
A、BC平分∠ABD B、AB=BD C、AE=BD D、BE=DE5. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G,若CG=3,AB=10,则△ABG的面积是( ) A、3 B、10 C、15 D、306. 作的角平分线的作图过程如下,用下面的三角形全等判定法则解释其作图原理,最为恰当的是( )
A、3 B、10 C、15 D、306. 作的角平分线的作图过程如下,用下面的三角形全等判定法则解释其作图原理,最为恰当的是( )作法:
. 在和上分别截取 , 使 .
. 分别以为圆心,以大于的长为半径作弧,两弧在内交于点 .
. 作射线 .
就是的平分线(如图).
 A、 B、 C、 D、7. 如图,以的顶点为圆心,任意长为半径画弧交 , 于点 , , 再分别以点、为圆心,大于的长为半径画弧,两弧在内部交于点 , 作射线 , 则下列说法错误的是( )
A、 B、 C、 D、7. 如图,以的顶点为圆心,任意长为半径画弧交 , 于点 , , 再分别以点、为圆心,大于的长为半径画弧,两弧在内部交于点 , 作射线 , 则下列说法错误的是( ) A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO交BC于点D.已知BD=5,CD=3,则点D到AB的距离为( )
A、 B、 C、 D、8. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AB,AC于点M,N,再分别以M,N为圆心,大于MN的长为半径画弧,两弧交于点O,作射线AO交BC于点D.已知BD=5,CD=3,则点D到AB的距离为( ) A、2 B、3 C、5 D、8
A、2 B、3 C、5 D、8二、填空题
-
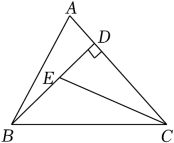
9. 如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=6,则△BCE的面积为 .
 10. 如图.四边形ABCD中.∠B=∠C=90°.AM、DM分别是∠DAB与∠ADC的平分线.AD=10.BC=6.则△ADM的面积为
10. 如图.四边形ABCD中.∠B=∠C=90°.AM、DM分别是∠DAB与∠ADC的平分线.AD=10.BC=6.则△ADM的面积为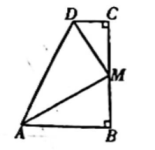 11. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.
11. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.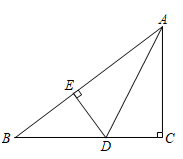 12. 如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为.
12. 如图,在△ABC中,AD为△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,若AB=5,AC=3,DF=2,则△ABC的面积为.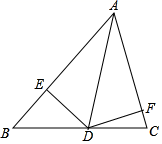 13. 如图,平分 , 点为上的任意一点, , 垂足为 , 线段的垂直平分线交于点 , 交于点 , 已知 , , 则的面积为 .
13. 如图,平分 , 点为上的任意一点, , 垂足为 , 线段的垂直平分线交于点 , 交于点 , 已知 , , 则的面积为 .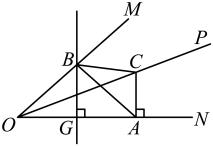
三、解答题
-
14. 如图,在△ABC中,∠ACB=90°,CE是斜边AB上的高,角平分线BD交CE于点M .
 (1)、求证:△CDM是等腰三角形.(2)、若AB=10,AC=8,求CM的长度.15. 如图,在中, , , 点D为边的中点,交的延长线于点E , 连接.
(1)、求证:△CDM是等腰三角形.(2)、若AB=10,AC=8,求CM的长度.15. 如图,在中, , , 点D为边的中点,交的延长线于点E , 连接. (1)、尺规作图:作的平分线交于点F;(保留作图痕迹)(2)、求证:;(3)、探究与之间的数量关系,并证明结论.
(1)、尺规作图:作的平分线交于点F;(保留作图痕迹)(2)、求证:;(3)、探究与之间的数量关系,并证明结论.四、综合题

