湘教版数学八年级下册 1.3 直角三角形全等的判定同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,已知 , 则证明≌的理由是( )
 A、 B、 C、 D、2. 如图,在∠ACB的两边上分别取点A,B使得CA=CB,将两个全等的直角三角板的直角顶点分别放在点A,B处,一条直角边分别落在∠ACB的两边上,另一条直角边交于点P,连接CP,则判定△ACP≌△BCP的依据是 ( )
A、 B、 C、 D、2. 如图,在∠ACB的两边上分别取点A,B使得CA=CB,将两个全等的直角三角板的直角顶点分别放在点A,B处,一条直角边分别落在∠ACB的两边上,另一条直角边交于点P,连接CP,则判定△ACP≌△BCP的依据是 ( ) A、AAS B、ASA C、SSS D、HL3. 如图,AB⊥CF , 垂足为B , DE⊥CF , 垂足为E , CB=FE , AC=DF , 依据上述条件可以判定△ABC≌△DEF , 这种判定三角形全等的依据是( )
A、AAS B、ASA C、SSS D、HL3. 如图,AB⊥CF , 垂足为B , DE⊥CF , 垂足为E , CB=FE , AC=DF , 依据上述条件可以判定△ABC≌△DEF , 这种判定三角形全等的依据是( ) A、AAS B、ASA C、SSS D、HL4. 如图,在中,点D在边上, , , , 垂足分别为E,F,.
A、AAS B、ASA C、SSS D、HL4. 如图,在中,点D在边上, , , , 垂足分别为E,F,.
求证:.以下是排乱的证明过程:
①∵在和中,
②∴.
③∴ ,
④∵ , ,
证明过程正确的顺序是( )
A、④→②→③→① B、④→③→①→② C、③→②→①→④ D、③→①→④→②5. 如图,在中,于点.如果 , 那么( ) A、 B、 C、 D、6. 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③BF//DE;④S△BEF=.其中所有正确结论的个数是( )
A、 B、 C、 D、6. 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③BF//DE;④S△BEF=.其中所有正确结论的个数是( ) A、1 B、2 C、3 D、47. 如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE=BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①∠ACN=∠BCN;②GF=EF;③∠GNC=120°;④GM=CN;⑤EG⊥AB,其中正确的个数是( )
A、1 B、2 C、3 D、47. 如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE=BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①∠ACN=∠BCN;②GF=EF;③∠GNC=120°;④GM=CN;⑤EG⊥AB,其中正确的个数是( ) A、2个 B、3个 C、4个 D、5个8. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )
A、2个 B、3个 C、4个 D、5个8. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )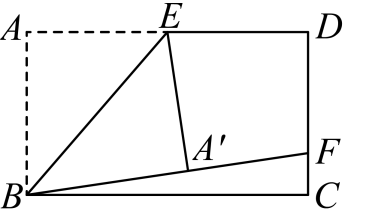 A、 B、8 C、12 D、16
A、 B、8 C、12 D、16二、填空题
-
9. 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,若DE=3cm,则BF=cm.
 10. 如图,有一个 , , , , 一条线段 , , 分别在和过点且垂直于的射线上运动, 时,才能使与全等.
10. 如图,有一个 , , , , 一条线段 , , 分别在和过点且垂直于的射线上运动, 时,才能使与全等. 11. 如图,在Rt中, , 两点分别在AC和过点且垂直于AC的射线AO上运动,当时,和全等.
11. 如图,在Rt中, , 两点分别在AC和过点且垂直于AC的射线AO上运动,当时,和全等. 12. 如图所示,在等腰△ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=73°,若点P是等腰△ABC的腰上的一点,则当△EDP为以DE为腰的等腰三角形时,∠EDP的度数是.
12. 如图所示,在等腰△ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=73°,若点P是等腰△ABC的腰上的一点,则当△EDP为以DE为腰的等腰三角形时,∠EDP的度数是. 13. 如图, 为 的角平分线,且 , 为 延长线上一点, ,过 作 于 ,下列结论:
13. 如图, 为 的角平分线,且 , 为 延长线上一点, ,过 作 于 ,下列结论:① ;② ;③ ;④ .
其中正确的序号是.

三、解答题
-
14. 如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,BE=DF,CE=CF.求证:AE=AF.
 15. 如图1,已知等边△ABC , 以B为直角顶点向右作等腰直角△BCD , 连接AD .
15. 如图1,已知等边△ABC , 以B为直角顶点向右作等腰直角△BCD , 连接AD . (1)、若 , 求点D到AB边的距离;(2)、如图2,过点B作AD的垂线,分别交AD , CD于点E , F , 探索EF , CF , BE之间的数量关系并证明;(3)、如图3,点M , N分别为线段AD , BD上一点,AM=BN , 连接CM , CN , 若 , 当CM+CN取得最小值时,直接写出△ACM的面积.(提示:直角三角形中两直角边的平方和等于斜边的平方)
(1)、若 , 求点D到AB边的距离;(2)、如图2,过点B作AD的垂线,分别交AD , CD于点E , F , 探索EF , CF , BE之间的数量关系并证明;(3)、如图3,点M , N分别为线段AD , BD上一点,AM=BN , 连接CM , CN , 若 , 当CM+CN取得最小值时,直接写出△ACM的面积.(提示:直角三角形中两直角边的平方和等于斜边的平方)四、综合题

