2023-2024学年湘教版初中数八年级下册 1.3 直角三角形全等的判定同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,已知AB⊥BD,CD⊥BD,若用“HL”判定 Rt△ABD和Rt△CDB 全等,则需要添加的条件是( )
 A、AD = CB B、∠A = ∠C C、BD = DB D、AB =CD2. 如图,最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是( )
A、AD = CB B、∠A = ∠C C、BD = DB D、AB =CD2. 如图,最适合用“HL”定理判定Rt△ABC和Rt△DEF全等的条件是( )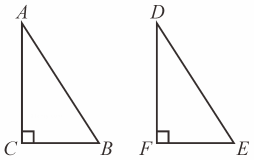 A、AC=DF,BC=EF. B、∠A=∠D,AB=DE. C、AC=DF,AB=DE. D、∠B=∠E,BC= EF.3. 如图,要用“”判定和全等的条件是( )
A、AC=DF,BC=EF. B、∠A=∠D,AB=DE. C、AC=DF,AB=DE. D、∠B=∠E,BC= EF.3. 如图,要用“”判定和全等的条件是( )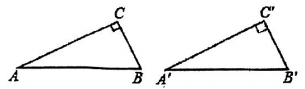 A、 , B、 , C、 , D、 ,4. 如图,已知点在同一条直线上, , 若添加一个条件后,能用“HL”的方法判定RtRt , 添加的条件可以是( )
A、 , B、 , C、 , D、 ,4. 如图,已知点在同一条直线上, , 若添加一个条件后,能用“HL”的方法判定RtRt , 添加的条件可以是( ) A、 B、 C、 D、5. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件中不能判定Rt△ABC≌Rt△A′B′C′的是( )A、AC=A′C′,∠B=∠B′ B、∠A=∠A′,∠B=∠B′ C、AB=A′B′,AC=A′C′ D、AB=A′B′,∠A=∠A′6. 如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )
A、 B、 C、 D、5. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件中不能判定Rt△ABC≌Rt△A′B′C′的是( )A、AC=A′C′,∠B=∠B′ B、∠A=∠A′,∠B=∠B′ C、AB=A′B′,AC=A′C′ D、AB=A′B′,∠A=∠A′6. 如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE,添加下列选项中的条件,能用HL判定△ABC≌△DEF的是( )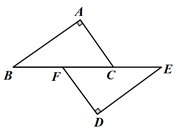 A、AC=DF B、∠B=∠E C、∠ACB=∠DFE D、BC=EF7. 如图,中, , , 以下结论中不一定正确的是( )
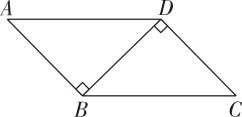
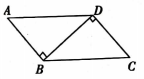
A、AC=DF B、∠B=∠E C、∠ACB=∠DFE D、BC=EF7. 如图,中, , , 以下结论中不一定正确的是( ) A、 B、是的角平分线 C、为的中点 D、8. 如图所示,P,Q分别是BC,AC上的点,作PR⊥AB于点R,作PS⊥AC于点S,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( )
A、 B、是的角平分线 C、为的中点 D、8. 如图所示,P,Q分别是BC,AC上的点,作PR⊥AB于点R,作PS⊥AC于点S,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.其中正确的是( ) A、①③ B、②③ C、①② D、①②③
A、①③ B、②③ C、①② D、①②③二、填空题
-
9. 如图,在四边形ABCD中,∠ABD=∠CDB=90°,根据“HL"添加条件可得△ABD≌△CDB .
 10. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.
10. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.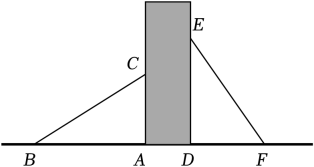 11. 如图,为中斜边上的一点,且 , 过点作的垂线,交于点 , 若 , , 则.
11. 如图,为中斜边上的一点,且 , 过点作的垂线,交于点 , 若 , , 则. 12. 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度与右边滑梯水平方向的长度相等,这两个滑梯与地面夹角中 , 则 .
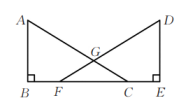
12. 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度与右边滑梯水平方向的长度相等,这两个滑梯与地面夹角中 , 则 . 13. 如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE , 若用“HL”判定△ABC≌△DEF , 则添加的一个条件是 .
13. 如图,点B、F、C、E在一条直线上,∠A=∠D=90°,AB=DE , 若用“HL”判定△ABC≌△DEF , 则添加的一个条件是 .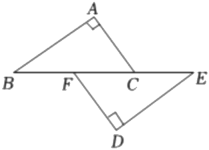
三、解答题