湘教版数学八年级下册 1.2 直角三角形的性质与判定(Ⅱ)同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 的三条边是 , 下列条件不能判断是直角三角形的是( )A、 B、 C、 D、2. 如图,在中, , , , 在线段BC上有一点D , , 连接AD , 则的面积为( )
 A、4 B、8 C、 D、103. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD , 对角线AC , BD交于点O . 若 , , 则等于( )
A、4 B、8 C、 D、103. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD , 对角线AC , BD交于点O . 若 , , 则等于( ) A、15 B、16 C、17 D、204. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kŭn,门槛的意思)一尺,不合二寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点、点与门槛的距离尺(1尺寸),则的长是( )
A、15 B、16 C、17 D、204. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kŭn,门槛的意思)一尺,不合二寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙寸,点、点与门槛的距离尺(1尺寸),则的长是( ) A、26寸 B、50.5寸 C、52寸 D、101寸5. 在学习勾股定理时,小明利用如图验证了勾股定理.若图中 , , 则阴影部分直角三角形的面积为( )
A、26寸 B、50.5寸 C、52寸 D、101寸5. 在学习勾股定理时,小明利用如图验证了勾股定理.若图中 , , 则阴影部分直角三角形的面积为( )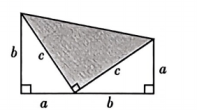 A、5 B、25 C、 D、6. 如图,在中,边的垂直平分线分别交 , 于点 , , 边的垂直平分线分别交 , BC于点N , F , 的周长为9.若 , , 则的面积为( )
A、5 B、25 C、 D、6. 如图,在中,边的垂直平分线分别交 , 于点 , , 边的垂直平分线分别交 , BC于点N , F , 的周长为9.若 , , 则的面积为( ) A、 B、 C、5 D、7. 如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=4 , ∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A、 B、 C、5 D、7. 如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=4 , ∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )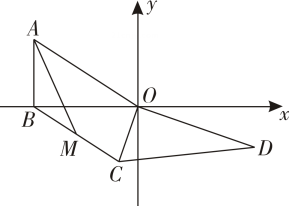 A、3 B、6-4 C、2-2 D、28. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 , , . 若 , 则下列关于 , , 的说法正确的是( )
A、3 B、6-4 C、2-2 D、28. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 , , . 若 , 则下列关于 , , 的说法正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,在中, , 以C为圆心,为半径画弧,交于点D , 再分别以为圆心,以大于为半径画弧,两弧相交于点M , 作直线交于点E . 若 , 则的面积是 .
 10. 如图,长方形的边长为3,长为1,在数轴上点A对应的数为 , 点B对应的数为2,以A为圆心,长为半径画弧,交数轴于点E , 则E点表示的数为 .
10. 如图,长方形的边长为3,长为1,在数轴上点A对应的数为 , 点B对应的数为2,以A为圆心,长为半径画弧,交数轴于点E , 则E点表示的数为 . 11. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是.
11. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=4,BC=2.运动过程中点D到点O的最大距离是.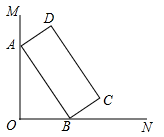 12. 如图,在Rt△ABC中,∠ABC=90°,∠A=30°,点D , E , F分别是线段AC , AB , DC的中点,下列结论:①△EFB为等边三角形.②S四边形DFBE=S△ABC . ③AE=2DF . ④AC=8DG . 其中正确的是 .
12. 如图,在Rt△ABC中,∠ABC=90°,∠A=30°,点D , E , F分别是线段AC , AB , DC的中点,下列结论:①△EFB为等边三角形.②S四边形DFBE=S△ABC . ③AE=2DF . ④AC=8DG . 其中正确的是 .
 13. 如图,在四边形中, , 点E在线段上运动,点F在线段上, , 则线段的最小值为 .
13. 如图,在四边形中, , 点E在线段上运动,点F在线段上, , 则线段的最小值为 .
三、解答题
-
14. 2023年7月五号台风“杜苏芮”登陆,使我国很多地区受到严重影响.据报道,这是今年以来对我国影响最大的台风,风力影响半径(即以台风中心为圆心,为半径的圆形区域都会受台风的影响).如图,线段BC是台风中心从C市向西北方向移动到B市的大致路线,A是某个大型农场,且 . 若A , C两地相距 , A , B两地相距 .

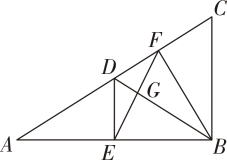
 (1)、农场A是否会受到台风的影响?请说明理由;(2)、若台风中心的移动速度为 , 则该农场受台风影响的持续时间有多长?15. 如图1,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G.
(1)、农场A是否会受到台风的影响?请说明理由;(2)、若台风中心的移动速度为 , 则该农场受台风影响的持续时间有多长?15. 如图1,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G. (1)、求证:△ACF≌△CBG;(2)、如图2,延长CG交AB于H,连接AG交CF于点M,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)、在(2)问的条件下,当∠FCH=2∠GAC时,若BG=4,求AM的长.
(1)、求证:△ACF≌△CBG;(2)、如图2,延长CG交AB于H,连接AG交CF于点M,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)、在(2)问的条件下,当∠FCH=2∠GAC时,若BG=4,求AM的长.四、综合题
-
16. 如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
 (1)、求BC,AC的长;(2)、若点D是射线OB上的一个动点,作直线DE⊥AC于点E,直线DE与直线BC交于点F.
(1)、求BC,AC的长;(2)、若点D是射线OB上的一个动点,作直线DE⊥AC于点E,直线DE与直线BC交于点F.①如图1,当点D在线段OB上时,求证:△BDF是等腰三角形;
②连结OF,CD,若S△OBF:S△OBC=1:2,求CD的长.
17. 阅读下面材料,并解决问题: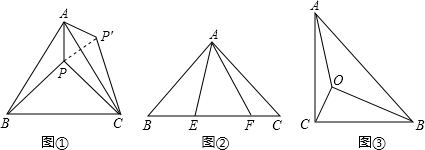 (1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
(1)、如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB=;
(2)、基本运用请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
(3)、能力提升如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.