湘教版数学八年级下册 1.2 直角三角形的性质与判定(Ⅱ)同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图,△ABC中,D为AC的中点,CE⊥AB于点E , 若DE=3,AE=5,则CE=( )
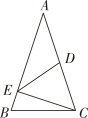 A、3 B、4 C、 D、
A、3 B、4 C、 D、 -
2. 在中, , , , 则的长为( )A、5 B、10 C、 D、28
-
3. 在中, , , 的对边分别是a , b , c , , 则该三角形的三边满足的关系是( )A、 B、 C、 D、
-
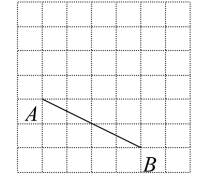
4. 如图是由边长为的方砖铺设的地板示意图,如果小球在地板上从点滚动到点 , 则小球滚动的最短路程是( )
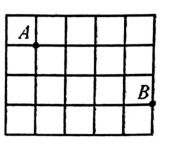 A、 B、 C、 D、
A、 B、 C、 D、 -
5. 如图,Rt△ABC中,∠ACB=90°,BC=4,AC=3,将△ABC绕点B逆时针旋转得 , 若点在AB上,则的长为( )
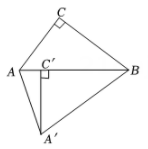 A、 B、4 C、 D、5
A、 B、4 C、 D、5 -
6. 将长方形纸片ABCD如图折叠,B , C两点恰好重合在AD边上的同一点P处,折痕分别是MH , NG , 若∠MPN=90°,PM=3,MN=5,分别记△PHM , △PNG , △PMN的面积为S1 , S2 , S3 , 则S1 , S2 , S3之间的数量关系是( )
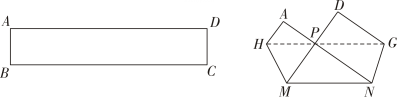 A、S3=S1+S2 B、3S3=2S1+2S2 C、S3=5S2-5S1 D、2S3=3S2-S1
A、S3=S1+S2 B、3S3=2S1+2S2 C、S3=5S2-5S1 D、2S3=3S2-S1 -
7. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图);如果大正方形的面积是 , 小正方形的面积是 , 直角三角形的两直角边分别为、 , 那么的值是( )
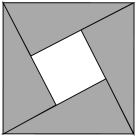 A、 B、 C、 D、
A、 B、 C、 D、 -
8. 如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点C′处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到C′处吃这块糖粒,已知盒子的长和宽为均为20cm,高为30cm,则蚂蚁爬行的最短距离为( )cm.
 A、10 B、50 C、10 D、70
A、10 B、50 C、10 D、70
二、填空题
-
9. 若直角三角形的两条直角边的长分别是3和4,则斜边上的中线长为.
-
10. 如图,一太阳能热水器支架(Rt△ACB)两直角边AC=1.2米,CB=1.6米,点D为受光面斜边AB的中点,则连杆CD的长为米.
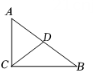
-
11. 如图,矩形纸片ABCD中,BC=8cm , 把矩形纸片沿直线BD折叠,点C落在点E处,BE交AD于点F , 若BF=cm , 则CD的长度为 .

-
12. 如图,CD为Rt△ABC斜边AB上的中线,E为AC的中点.若 , , 则DE= .

-
13. 如图,点O为等边△ABC内一点AO=8,BO=6,CO=10,将△AOC绕点A顺时针方向旋转60°,使AC与AB重合,点O旋转至点O1处,连接OO1 , 则四边形AO1BO的面积是 .