湘教版数学八年级下册 1.1 直角三角形的性质与判定（Ⅰ）同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ C = 60 °$ ， $A D ⊥ B C$ ， $A E = D E$ ，连接 $B E$ 并延长交 $A C$ 于点 $F$ ，若 $∠ A F B = 90 °$ ， $E F = 3$ ，则 $B F$ 的长为（）

A、15 B、20 C、9 D、12

查看试题解析
3. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， ∠ A = 30 ° ， C D ⊥ A B$ 于点 $D$ ，则 $△ A B C$ 与 $△ B C D$ 的周长之比为（）

A、 $2 ： 1$ B、 $3 ： 1$ C、 $4 ： 1$ D、 $5 ： 1$

查看试题解析
4. 如图，在四边形ABCD中，∠ABC=∠ADC=90°，E为对角线AC的中点，连接BE，DE，若∠BAD=58°，则∠BED的度数为(　　)

A、118° B、108° C、122° D、116°

查看试题解析
5. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $D$ 为线段 $C A$ 延长线一点， $F$ 为线段 $B C$ 上一点，连接 $D F$ 交 $A B$ 于点 $G$ ，连接 $C G$ ，若 $B F = \sqrt{3} A D$ ，设 $∠ D = x$ ，则 $∠ B G C$ 可表示为（）

A、 $750 °$ B、 $45 ° + 2 x$ C、 $60 ° + x$ D、 $90 ° - 2 x$

查看试题解析
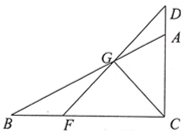6. 如图，在Rt△ABC中，∠BAC＝90°，∠C＝30°，将边AB沿着AE翻折，使点B落在BC上的点D处，再将边AC沿着AF翻折，使得C落在AD延长线上的点C′处，两条折痕与斜边BC分别交于E ， F ．以下四个结论正确的是（）
①∠EAF＝45°；②FC′＝BE；③EC＝3BE；④FC＝( $\sqrt{3}$ －1)AE ．

A、①②③ B、②④ C、①③④ D、①②③④

查看试题解析
7. 如图，将边长为 $\sqrt{3}$ 的正方形 $A B C D$ 绕点 $B$ 逆时针旋转 $30 °$ 得到正方形 $A' B C' D'$ ， $A D$ 与 $C' D'$ 交于点 $M$ ，那么图中点 $M$ 的坐标为（）

A、 $(\sqrt{3} ， 1)$ B、 $(1 ， \sqrt{3})$ C、 $(\sqrt{3} ， \frac{\sqrt{3}}{2})$ D、 $(\frac{\sqrt{3}}{2} ， \sqrt{3})$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A C = B C$ ， $A M$ 为 $△ A B C$ 的角平分线， $D$ 为 $A B$ 的中点， $A M$ 与 $C D$ 相交于点 $P$ ，过点 $D$ 作 $D E$ 垂直 $A M$ 于点 $E$ ，过点 $E$ 作 $E N ∥ A C$ 交 $A B$ 于点 $N$ ，有下列说法：① $∠ 1 + ∠ 2 > 90 °$ ． ② $∠ A D E = ∠ E D C + ∠ A C D$ ， ③ $N$ 为 $A D$ 的中点，④ $S_{△ B P C} = S_{△ A P C}$ ．其中，正确的是（　　）

A、①③ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

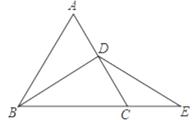
9. 如图，△ABC是等边三角形，BD平分∠ABC，点E在BC的延长线上，且CE＝1，∠E＝30°，则BC＝.

查看试题解析
10.
如图，在△ABC中，∠C=90°，∠B=20°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB= ．

查看试题解析
11. 如图， $∠ A C B = 9 0^{°} ， C D ⊥ A B$ ，垂足为 $D$ .

(1)、图中有个直角三角形.

(2)、 $∠ A$ 的余角有；与 $∠ A$ 相等的角有.

(3)、若 $B D = 2 ， ∠ 2 = 3 0^{°}$ ，则 $A B =$ .

查看试题解析
12. 如图，在Rt $△ A B C$ 中， $∠ B A C = 9 0^{°} ， A D$ 为斜边上的中线，将 $△ A D C$ 沿AD翻折，使点 $C$ 落在 $△ A B C$ 所在平面的点 $C^{^{'}}$ 处，若 $A C^{^{'}}$ $/ / B C$ ，则 $∠ B =$ .

查看试题解析
13. 如图，在等腰三角形ABC中，AC＝BC＝4，∠A＝30°，点D为AC的中点，点E为边AB上一个动点，连接DE，将△ADE沿直线DE折叠，点A落在点F处.当直线EF与直线AC垂直时，则AE的长为.

查看试题解析

三、解答题

14. 已知：如图，在 $Δ B C D$ 中， $C E ⊥ B D$ 于点 $E$ ，点 $A$ 是边 $C D$ 的中点， $E F$ 垂直平分线段 $A B$ ．

(1)、求证： $B E = \frac{1}{2} C D$ ；

(2)、当 $A B = B C$ ， $∠ A B D = 25 °$ 时，求 $∠ A C B$ 的度数．

查看试题解析
15. 探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．
如下图，将两个完全相同的三角形纸片 $△ A B C$ 和 $△ D E C$ 重合放置，其中 $∠ C = 90 °$ ．若固定 $△ A B C$ ，将 $△ D E C$ 绕点C旋转．


(1)、当 $△ D E C$ 绕点C旋转到点D恰好落在 $A B$ 边上时，如下图．

①当 $∠ B = ∠ E = 40 °$ 时，求此时旋转角的大小；
②当 $∠ B = ∠ E = α$ 时，直接写出此时旋转角的大小(用含α的式子表示)．

(2)、当 $△ D E C$ 绕点C旋转到如下图所示的位置时，小组长猜想： $△ B D C$ 的面积与 $△ A E C$ 的面积相等，试判断小组长的猜想是否正确，若正确，请你证明小组长的猜想．若不正确，请说明理由．


查看试题解析

四、综合题

16. 如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E.

(1)、求证：AE=2CE；

(2)、连接CD，请判断△BCD的形状，并说明理由.

查看试题解析