2023-2024学年湘教版初中数八年级下册 1.1 直角三角形的性质与判定（Ⅰ）同步分层训练基础题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. $△ A B C$ 中，如果 $∠ A + ∠ B = ∠ C$ ，那么 $△ A B C$ 的形状是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
2. 根据图中给定的条件，下列各图中可以判断 $∠ 1$ 与 $∠ 2$ 一定相等的是（）

A、 $① ②$ B、 $① ③$ C、 $① ② ③$ D、 $① ② ③ ④$

查看试题解析
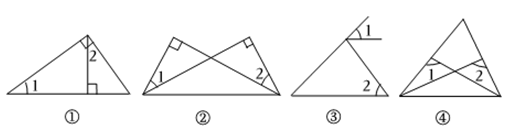3. 已知△ABC中，∠A，∠B，∠C三个角的比例如下，其中能说明△ABC是直角三角形的是（）

A、2：3：4 B、1：2：3 C、4：3：5 D、1：2：2

查看试题解析
4. 如图，已知AC⊥BC于点C，CD⊥AB于点D，∠A=56°，则∠DCB的度数是（）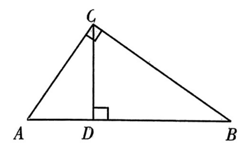

A、30° B、45° C、56° D、60°

查看试题解析
5. 已知下列命题，其中原命题与逆命题均为真命题的有（    ）
①若 $a > b$ ，则 $a c > b c$ ；        ②两直线平行，内错角相等；
③直角三角形的两个锐角互余；        ④全等三角形的周长相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ B = 30 °$ ， AD是斜边BC上的高，若 $C D = 3$ ，则BD的长为（）

A、3 B、6 C、9 D、12

查看试题解析
7. 5月26日，“2023中国国际大数据产业博览会”在贵阳开幕，在“自动化立体库”中有许多几何元素，其中有一个等腰三角形模型（示意图如图所示），它的顶角为 $120 °$ ，腰长为 $12 m$ ，则底边上的高是（）

A、 $4 m$ B、 $6 m$ C、 $10 m$ D、 $12 m$

查看试题解析
8. 如图，在四边形 $A B C D ， D A ⊥ A B ， D A = 6 c m ， ∠ B + ∠ C = 150 ° ， A$ 刚好是 $E B$ 中点，P、Q分别是线段 $C E 、 B E$ 上的动点，则 $B P + P Q$ 的最小值为（）

A、12 B、15 C、16 D、18

查看试题解析

二、填空题

9. 如图，在 $△ A B C$ 中， $∠ B = 30 °$ ， $B C$ 的垂直平分线交 $A B$ 于点E ，垂足为D.若 $E D = 5$ ，则 $E C$ 的长为.

查看试题解析
10. 如图，在等边 $△ A B C$ 中， $A B = 8$ ， $A H ⊥ B C$ 于点H ， P为 $A H$ 上的一个动点，以 $C P$ 为一边作等边 $△ C P Q$ ，连接 $H Q$ ．在P点的运动过程中线段 $H Q$ 的最小值为．

查看试题解析
11. 如图，在 $△ A B C$ 中， $∠ B = ∠ C = 60 °$ ，点D为 $A B$ 边的中点， $D E ⊥ B C$ 于E ，若 $B E = 2$ ，则 $A C$ 的长为．

查看试题解析
12. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 30 °$ ， $A C = 2$ ， $B C = 2 \sqrt{3}$ ，将 $△ A B C$ 绕点C逆时针旋转至 $△ A^{'} B^{'} C$ ，使得点 $A^{'}$ 恰好落在AB上， $A^{'} B^{'}$ 与BC交于点D，则 $△ A^{'} C D$ 的面积为.

查看试题解析
13. 如图，将一副三角尺如图所示叠放在一起，若AB＝12cm，则阴影部分的面积是cm² ．

查看试题解析

三、解答题

14. 如图，在 $△ A B C$ 中， $A B = A C = 8$ ， $∠ C B A = 45 °$

(1)、求证： $A C ⊥ A B$ ；

(2)、以AC为边，作等边三角形 $△ A C D$ ，且点D在AC的左侧，连接CD ， AD ， BD.求 $△ A B D$ 的面积.

查看试题解析
15. 如图，在 $△ A B C$ 中，D为 $A B$ 边上一点， $D F ⊥ B C$ 于F ，延长 $F D 、 C A$ 交于E ．若 $∠ E = 30 ° ， A D = A E$ ．

(1)、求证： $△ A B C$ 为等边三角形；

(2)、若D是 $A B$ 的中点，求 $\frac{D E}{D F}$ 的值．

查看试题解析

四、综合题

16. 如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E.

(1)、求∠CBE的度数；

(2)、过点D作DF∥BE，交AC的延长线于点F，求∠F的度数.

查看试题解析