2023-2024学年湘教版初中数学七年级下册 2.2.3 运用乘法公式进行计算同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $(- 3 a b)^{2} = 9 a^{2} b^{2}$ C、 $(a + b)^{2} = a^{2} + b^{2}$ D、 $a^{3} + a^{3} = 2 a^{6}$

查看试题解析
2. 运用完全平方公式（a+b）²=a²+2ab+b²计算（x+ $\frac{1}{2}$ ）² ，则公式中的2ab是（）

A、 $\frac{1}{2} x$ B、x C、2x D、4x

查看试题解析
3. 若k为任意整数，则（2k+3）²-4k²的值总能（）

A、被2整除． B、被3整除． C、被5整除． D、被7整除．

查看试题解析
4. 国际数学家大会是数学界的最高水平盛典，大合邀请著名数学粽子者，交流报告数学最新迸展和成果，由承办国的国泉元曾颁发世界数学最高奖——菲尔兹奖.2002年在北京召开了国数学家大会，会标图案是我国古代著名的”赵爽弦图”．图中包合四个面积为24的全等的直角三角形，围成的大正方形面积为100．则直角三角形中较长直角边与较短直角边的长度差为（）

A、2 B、4 C、6 D、8

查看试题解析
5. 如图，正方形ABCD和长方形AEFG的面积相等，且四边形BEFH也是正方形，欧几里得在《几何原本》中利用该图得到了：BH²=CH×GH．设AB=a，CH=b.若ab=5，则图中阴影部分的周长是（　　）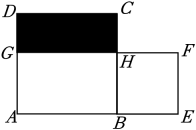

A、6 B、8 C、10 D、20

查看试题解析
6. 用公式法分解因式：① $x^{2} + x y + y^{2} = {(x + y)}^{2}$ ；② $- x^{2} + 2 x y - y^{2} = - {(x - y)}^{2}$ ；③ $x^{2} + 6 x y - 9 y^{2} = {(x - 3 y)}^{2}$ ；④ $- x^{2} + \frac{1}{4} = (\frac{1}{2} + x) (\frac{1}{2} - x)$ ，其中正确的有（）个

A、1 B、2 C、3 D、4

查看试题解析
7. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“完美数”，如 $12 = 4^{2} - 2^{2}$ ， $52 = 1 4^{2} - 1 2^{2}$ ，因此12，52这两个数都是“完美数”，则下列结论中错误的是（）

A、20是“完美数” B、最小的“完美数”是4 C、“完美数”一定是4的奇数倍 D、小于30的所有“完美数”之和是60

查看试题解析
8. 现有一张边长为a的大正方形卡片和三张边长为b的小正方形卡片（ $\frac{1}{2} a < b < a$ ）如图1，取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图2，再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图3．已知图3中的阴影部分的面积比图2中的阴影部分的面积大 $2 a b - 6$ ，则小正方形卡片的面积是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

9. 计算 $2019 \times 2017 - 201 8^{2} =$ ．

查看试题解析
10. 若要使4x²+mx+ $\frac{1}{64}$ 成为一个两数差的完全平方式，则m的值应为

查看试题解析
11. 如图，“赵爽弦图”由4个全等的直角三角形所围成，在Rt△ABC中，AC＝b，BC＝a，∠ACB＝90°，若图中大正方形的面积为42，小正方形的面积为5，则（a+b）²的值为．

查看试题解析
12. 计算： $2 (1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) + \frac{1}{2^{14}} =$ ．

查看试题解析
13. 已知 $N = (2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) (2^{16} + 1)$ ，则 $N$ 的个位数字是．

查看试题解析

三、解答题

14. 阅读材料，解决后面的问题：
若 $m^{2} + 2 m n + 2 n^{2} - 6 n + 9 = 0$ ，求 $m - n$ 的值．
解： $∵ m^{2} + 2 m n + 2 n^{2} - 6 n + 9 = 0$ ，
$∴ (m^{2} + 2 m n + n^{2}) + (n^{2} - 6 n + 9) = 0$ ，
即： $(m + n)^{2} + (n - 3)^{2} = 0$ ， $∴ m + n = 0$ ， $n - 3 = 0$ ，
解得： $m = - 3$ ， $n = 3$ ， $∴ m - n = - 3 - 3 = - 6$ ．

(1)、若 $x^{2} + y^{2} + 6 x - 8 y + 25 = 0$ ，求 $x + 2 y$ 的值；

(2)、已知等腰 $△ A B C$ 的两边长 $a$ ， $b$ ，满足 $a^{2} + b^{2} = 10 a + 12 b - 61$ ，求该 $△ A B C$ 的周长；

(3)、已知正整数 $a$ ， $b$ ， $c$ 满足不等式 $a^{2} + b^{2} + c^{2} + 36 < a b + 6 b + 10 c$ ，求 $a + b - c$ 的值．

查看试题解析
15. 阅读下面计算过程：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ ；
请解决下列问题：

(1)、化简： $\frac{1}{\sqrt{3} + 2} =$ ；

(2)、根据上面的规律，请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(3)、利用上面的解法，请化简： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2023}}$ ．

查看试题解析

四、综合题

16. 如图1，有A型、B型、C型三种不同形状的纸板，A型是边长为a的正方形，B型是边长为b的正方形，C型是长为b，宽为a的长方形．现用A型纸板一张，B型纸板一张，C型纸板两张拼成如图2的大正方形．

(1)、观察图2，请你用两种方法表示出图2的总面积．
方法1：；
方法2：；
请利用图2的面积表示方法，写出一个关于a，b的等式：．

(2)、已知图2的总面积为 $49$ ，一张A型纸板和一张B型纸板的面积之和为 $25$ ，求 $a b$ 的值．

(3)、用一张A型纸板和一张B型纸板，拼成图3所示的图形，若 $a + b = 8$ ， $a b = 15$ ，求图3中阴影部分的面积．

查看试题解析
17. 【知识生成】通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式．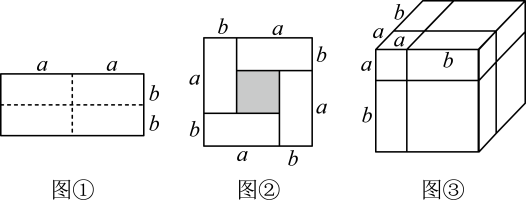
例如：如图①是一个长为 $2 a$ ，宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：

(1)、请用两种不同的方法求图②中阴影部分的面积：
方法1：；
方法2：；
由此可以得出 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据图③，写出一个代数恒等式：；

(3)、已知 $a + b = 3$ ， $a b = 1$ ，利用上面的规律求 $\frac{a^{3} + b^{3}}{2}$ 的值．

查看试题解析