2023-2024学年湘教版初中数学七年级下册 2.2.2 完全平方公式同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知（a+b）²＝49，a²+b²＝25，则ab＝（）

A、24 B、48 C、12 D、2 $\sqrt{6}$

查看试题解析
2. 已知 $x - \frac{1}{x} = 2$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
3. 如果 $x^{2} + (m - 1) x + 9$ 是一个完全平方式，那么m的值是（）

A、7 B、-7 C、-5或7 D、-5或5

查看试题解析
4. 将多项式4x²+1再加上一项，使它能分解因式成（a+b）²的形式，以下是四位学生所加的项，其中错误的是（）

A、2x B、﹣4x C、4x⁴ D、4x

查看试题解析
5. 整式 $x^{2} + 4 x + m$ 为某完全平方式展开后的结果，则 $m$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
6. 若( $\frac{1}{3}$ m-y)²= $\frac{1}{9}$ m²+ $\frac{1}{5}$ mx+ $\frac{1}{16}$ ，则x、y的值分别为（）

A、 $- \frac{5}{6}$ ， $\frac{1}{4}$ 或 $\frac{5}{6}$ ， $- \frac{1}{4}$ B、 $- \frac{5}{6}$ ， $\frac{1}{4}$ C、 $\frac{5}{6}$ ， $- \frac{1}{4}$ D、 $\frac{5}{6}$ ， $\frac{1}{4}$

查看试题解析
7. 已知x+y=3，x³+y³=9，则x⁷+y⁷=（）．

A、129 B、225 C、125 D、675

查看试题解析
8. 关于 $x$ 的多项式： $a_{n} x^{n} + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + ⋯ + a_{2} x^{2} + a_{1} x + a_{0}$ ，其中 $n$ 为正整数，若各项系数各不相同且均不为0，我们称这样的多项式为“亲缘多项式”．
① ${(2 x - 1)}^{2}$ 是“亲缘多项式”．
②若多项式 $a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ 和 $b_{4} x^{4} + b_{3} x^{3} + b_{2} x^{2} + b_{1} + b_{0}$ 均为“亲缘多项式”，则 $a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0} + b_{4} x^{4} + b_{3} x^{3} + b_{2} x^{2} + b_{1} + b_{0}$ 也是“亲缘多项式”．
③多项式 ${(2 x - 1)}^{4} = b_{4} x^{4} + b_{3} x^{3} + b_{2} x^{2} + b_{1} x + b_{0}$ 是“亲缘多项式”且 $b_{4} + b_{2} + b_{0} = 41$ ．
④关于 $x$ 的多项式 ${(a x + b)}^{n}$ ，若 $a \neq b$ ， $a b \neq 0$ ， $n$ 为正整数，则 ${(a x + b)}^{n}$ 为“亲缘多项式”．
以上说法中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 已知a²+b²=25，且ab=12，则a-b= ．

查看试题解析
10. 已知a+ $\frac{1}{a}$ =3，则a²+ $\frac{1}{a^{2}}$ 的值是．

查看试题解析
11. 已知大长方形的长为a，宽为b (a≠2b)，三个形状和大小都相同的小长方形按如图的方式放置在大长方形内，若x、y表示小长方形的长和宽，给出下列四个等式：．
①x-y=a-b；
②x²-y²= $\frac{a^{2} - b^{2}}{3}$
③(x+y)²= $\frac{a b}{2}$
④ $\frac{x}{y} = \frac{2 a - b}{2 b - a}$

其中等式成立的有(填序号)

查看试题解析
12. 已知a＝2023x+2023，b＝2023x+2024，c＝2023x+2025，则a²+b²+c²-ab-ac-bc的值是．

查看试题解析
13. $m > 0$ ， $n > 0$ ，若 $m^{2} + 4 n^{2} = 13$ ， $m n = 3$ ，请借助下图直观分析，通过计算求得 $m + 2 n$ 的值为．

查看试题解析

三、解答题

14. 阅读下列材料，完成下列任务．
小丽在数学资料上看到这样一道题：
已知x＝ $\sqrt{2}$ ＋1，求代数式x²－2x－1的值．
解：∵x＝ $\sqrt{2}$ ＋1，∴x－1＝ $\sqrt{2}$ ，
∴（x－1）²＝（ $\sqrt{2}$ ）² ， ∴x²－2x＋1＝2，∴x²－2x＝1，
∴x²－2x－1＝1－1＝0.
任务：

(1)、在材料解答过程中，主要用了我们学过的数学知识是（____）

A、平方差公式 B、完全平方公式 C、因式分解 D、单项式与多项式的乘法

(2)、在材料解答的过程中，主要用的思想方法是（____）

A、整体与化归思想 B、方程思想 C、分类讨论思想 D、数形结合思想

(3)、已知x＝ $\sqrt{3}$ －2，求x²＋4x－4的值．

查看试题解析
15. 如图1是一个长为 $4 a$ 、宽为 $b$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）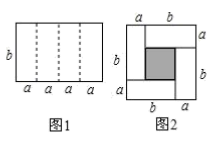

(1)、观察图2请你写出 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5$ ， $x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 ${(2019 - m)}^{2} + {(m - 2020)}^{2} = 15$ ，求 $(2019 - m) (m - 2020)$ 的值．

查看试题解析

四、综合题

16. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了(a+b)ⁿ(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律．例如，在三角形中第三行的三个数1，2， 1，恰好对应(a+b)²=a²+2ab+b²展开式中的系数；第四行的四个数1，3，3，1，恰好对应着(a+b)³=a³+3a²b+3ab²+b³展开式中的系数等等．

(1)、根据上面的规律，写出(a+b)⁵的展开式．

(2)、利用上面的规律计算：2⁵-5×2⁴+10×2³-10×2²+5×2-1．

查看试题解析
17. 图1是一个长为 $4 b$ ，宽为 $a (a > b)$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按如图2所示的形状拼成一个大正方形．

(1)、图2中的阴影部分正方形的边长是（用含a，b的代数式表示）；

(2)、观察图1，图2，请写出 $(a + b)^{2} ， (a - b)^{2}$ ， $a b$ 之间的等量关系是：

(3)、已知 $(m + n)^{2} = 25 ， (m - n)^{2} = 16$ ，求 $m^{2} + n^{2}$ 的值．

(4)、如图3，C是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向上分别作正方形 $A C D E$ 和正方形 $B C F G$ ，连接 $A F$ ．若 $A B = 7 ， D F = 3$ ，求 $△ A F C$ 的面积．

查看试题解析