2023-2024学年湘教版初中数学七年级下册 2.2.1 平方差公式同步分层训练培优题
试卷更新日期:2024-01-26 类型:同步测试
一、选择题
-
1. 若k为任意整数,则的值总能( )A、被2整除 B、被3整除 C、被5整除 D、被7整除2. 对于(2a+3b-1)(2a-3b+1),为了用平方差公式计算,下列变形正确的是( )A、[2a-(3b+1)]2 B、[2a+(3b-1)][2a-(3b-1)] C、[(2a-3b)+1][(2a-3b)-1] D、[2a-(3b-1]23. 从边长为的大正方形纸板挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
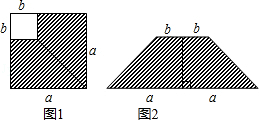
 A、 B、 C、 D、4. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证 ( )
A、 B、 C、 D、4. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证 ( ) A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2﹣2ab+b2 C、(a+2b)(a﹣b)=a2+ab﹣2b2 D、a2﹣b2=(a+b)(a﹣b)5. 如图,阴影部分是在一个边长为的大正方形中剪去一个边长为的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形.给出下列四种割拼方法,每种割拼方法都能够验证平方差公式,其中用到的数学思想是( )
A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2﹣2ab+b2 C、(a+2b)(a﹣b)=a2+ab﹣2b2 D、a2﹣b2=(a+b)(a﹣b)5. 如图,阴影部分是在一个边长为的大正方形中剪去一个边长为的小正方形后得到的图形,将阴影部分通过割、拼,形成新的图形.给出下列四种割拼方法,每种割拼方法都能够验证平方差公式,其中用到的数学思想是( ) A、数形结合思想 B、整体思想 C、公理化思想 D、方程思想6. 式子化简的结果为( )A、 B、 C、 D、7. (2+1)(22+1)(24+1)…(216+1)的结果为( )A、232-1 B、232+1 C、232 D、2168. 如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( )
A、数形结合思想 B、整体思想 C、公理化思想 D、方程思想6. 式子化简的结果为( )A、 B、 C、 D、7. (2+1)(22+1)(24+1)…(216+1)的结果为( )A、232-1 B、232+1 C、232 D、2168. 如图,把一块面积为100的大长方形木板被分割成2个大小一样的大正方形①,1个小正方形②和2个大小一样的长方形③后,如图摆放,且每个小长方形③的面积为16,则标号为②的正方形的面积是( ) A、16 B、14 C、12 D、10
A、16 B、14 C、12 D、10二、填空题
-
9. 若 , 则代数式的值为 .10. 某学校改造一个边长为5x米的正方形花坛,经规划后,南北向要缩短3米,东西向要加长3米,则改造后花坛的面积是平方米,改造后花坛的面积减少了平方米.11. 如图①,在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩下部分沿图中虚线剪开后拼成如图②所示的梯形、通过计算图①、图②中阴影部分的面积,可以得到的代数恒等式为 .
 12. 观察下列各式的规律:;;;请将发现的规律用含的式子表示为 .13. 若一个四位正整数 满足:a+c=b+d , 我们就称该数是“交替数”,则最小的“交替数”是 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 .
12. 观察下列各式的规律:;;;请将发现的规律用含的式子表示为 .13. 若一个四位正整数 满足:a+c=b+d , 我们就称该数是“交替数”,则最小的“交替数”是 ;若一个“交替数”m满足千位数字与百位数字的平方差是15,且十位数字与个位数的和能被5整除.则满足条件的“交替数”m的最大值为 .三、解答题
-
14. 如图,图1为边长为a的大正方形中有一个边长为b的小正方形,图2是由图1中的阴影部分拼成的一个长方形.
 (1)、设图1中阴影部分的面积为 , 图2中阴影部分的面积为 , 则 , (请用含a , b的代数式表示,只需表示,不必化简).(2)、以上结果可以验证哪个乘法公式?这个乘法公式是(3)、运用(2)中得到的公式,计算: .15. 观察以下等式:
(1)、设图1中阴影部分的面积为 , 图2中阴影部分的面积为 , 则 , (请用含a , b的代数式表示,只需表示,不必化简).(2)、以上结果可以验证哪个乘法公式?这个乘法公式是(3)、运用(2)中得到的公式,计算: .15. 观察以下等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
按照以上规律,解决下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第个等式(用含的式子表示),并证明.四、综合题
