2023-2024学年湘教版初中数学七年级下册 2.2.1 平方差公式同步分层训练基础题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 计算(2x-5)(2x-5)的结果是（）

A、4x²-5 B、4x²-25 C、25-4x² D、4x²+25

查看试题解析
2. 若a²-b²= $\frac{1}{4}$ ， a-b= $\frac{1}{2}$ ，则a+b的值为（）

A、 $- \frac{1}{2}$ B、1 C、 $\frac{1}{2}$ D、2

查看试题解析
3. 如图，在边长为a的正方形中，剪去一个边长为x的小正方形，将余下部分对称剪开，拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a，x的恒等式是（）

A、 $a^{2} - x^{2} = (2 x + 2 a) (a - x)$ B、 $a^{2} - x^{2} = \frac{1}{2} (x + a) (a - x)$ C、 $(a - x)^{2} = (x + a) (x - a)$ D、 $a^{2} - x^{2} = (x + a) (a - x)$

查看试题解析
4. 下列各式中，能用平方差公式计算的是（）

A、 ${(a + b)}^{2}$ B、 $(a + b) (a - b)$ C、 ${(a - b)}^{2}$ D、 $(- a + b) (a - b)$

查看试题解析
5. 如图，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（）

A、（a﹣b）²=a²﹣2ab+b² B、（a+b）²=a²+2ab+b² C、a²﹣b²=（a+b）（a﹣b） D、无法确定

查看试题解析
6. 边长为m的正方形边长增加n以后，所得较大正方形的面积比原正方形面积增加了（）

A、n² B、2mn C、2mn-n² D、2mn+n²

查看试题解析
7. 观察下面图形，从图1到图2可用式子表示为（）

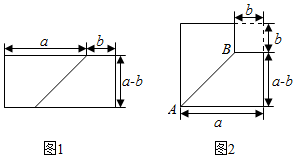A、（a+b）（a﹣b）＝a²﹣b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+2ab+b²＝（a+b）²

查看试题解析
8. 从前，古希腊一位庄园主把一块边长为a米（a＞6）的正方形土地租给租户王老汉，第二年，他对王老汉说：“我把这块地的一边增加6米，相邻的另边减少6米，变成矩形土地继续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得王老汉的租地面积会（）

A、没有变化 B、变大了 C、变小了 D、无法确定

查看试题解析

二、填空题

9. 已知： $x + y = - 5$ ， $x - y = 2$ ，则 $x^{2} - y^{2} =$ ．

查看试题解析
10. 计算：（a+1）（a﹣1）=.

查看试题解析
11. 已知a+b=3，ab=﹣2，则a²+b²的值是．

查看试题解析
12. 请你观察如图的图形，依据图形面积的关系，不需要添加辅助线，便可得到一个非常熟悉的乘法公式，这个公式是.

查看试题解析
13. 填空：

(1)、( $\frac{1}{2}$ x+ $\frac{2}{3}$ y)()= $\frac{1}{4}$ x²- $\frac{4}{9}$ y²

(2)、()( $\frac{1}{2}$ m+ $\frac{2}{5}$ n)= $\frac{1}{4}$ m²- $\frac{4}{25}$ n² ．

(3)、(-5s+6t)()= 25s²-36t² ．

(4)、( $\frac{1}{2}$ +)(- $\frac{1}{2}$ )= $\frac{1}{25}$ x²- $\frac{1}{4}$

查看试题解析

三、解答题

14. 通过学习，同学们已经体会到灵活运用乘法公式使整式的乘法运算方便、快捷．相信通过对下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．例：用简便方法计算： $195 \times 205$ ．
解： $195 \times 205$ ，
$= (200 - 5) (200 + 5)$ ①
$= 20 0^{2} - 5^{2}$ ②
$= 39975$ ．

(1)、例题求解过程中，由①到②变形是利用（填乘法公式的名称）．

(2)、用简便方法计算： $9 \times 11 \times 101 \times 10001$ ．

查看试题解析
15. 如图，将两个长方形用不同方式拼成图 $1$ 和图 $2$ 两个图形．

(1)、若图 $1$ 中的阴影部分面积为 $a^{2} - b^{2}$ ，则图 $2$ 中的阴影部分面积为 $($ 用含字母 $a$ ， $b$ 的代数式表示 $)$ ；

(2)、由 $(1)$ 你可以得到的等式是；

(3)、根据你所得到的等式解决下面的问题：
$①$ 若 $x^{2} - y^{2} = 16$ ， $x - y = 2$ ，则 $x + y =$ _▲_ ；
$②$ 计算： $77.7 5^{2} - 22.2 5^{2}$ ．
$③$ 解方程： $(x + 1)^{2} - (x - 1)^{2} = - 8$ ．

查看试题解析

四、综合题

16. 如图①，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿线剪开，如图所示，拼成图②的长方形．

(1)、请你表示出图①中阴影部分的面积；
请你表示出图②中阴影部分的面；

(2)、比较两图的阴影部分面积，可以得到乘法公式：；

(3)、请应用公式计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) ⋯ (1 - \frac{1}{202 2^{2}}) (1 - \frac{1}{202 3^{2}})$ ．

查看试题解析
17. 探究活动：

(1)、如图①，可以求出阴影部分的面积是（写成两数平方差的形式）；

(2)、如图②，若将图①中阴影部分裁剪下来，重新拼成一个长方形，面积是（写成多项式乘法的形式）；

(3)、比较图①，图②阴影部分的面积，可以得到公式．

(4)、计算：① $(a + b - 2 c) (a + b + 2 c)$ ；
② $(2 a + b - 3 c) (- 2 a + b + 3 c)$ ．

查看试题解析