2023-2024学年湘教版初中数学七年级下册 2.1.4 多项式的乘法同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 要使多项式 $(x + m) (x - 2)$ 不含x的一次项，则m的值为（）

A、0 B、1 C、2 D、 $- 2$

查看试题解析
2. 若 $(x + a) (x - b)$ 的积中不含 $x$ 的一次项，那么 $a$ 与 $b$ 一定是（）

A、互为相反数 B、互为倒数 C、相等 D、 $a$ 比 $b$ 大

查看试题解析
3. 已知(x+a)(x+b)=x²+mx+24，其中a，b为整数，则整数m可能的取值有（）个.

A、2 B、4 C、6 D、8

查看试题解析
4. 如图1，有边长分别为a和b（a>b）的A类和B类正方形纸片、长为a、宽为b的C类矩形纸片若干张，要拼一个边长为a+b的正方形（如图2所示），则需要1张A类纸片、1张B类纸片和⒉张C类纸片.若要拼一个长为3a+b、宽为2a+2b的矩形，则需要C类纸片的张数为（）

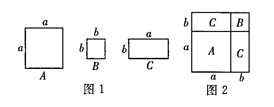A、6 B、7 C、8 D、9

查看试题解析
5. (x-a)(x²+ax+a²)的计算结果是（）

A、x³+2ax+a³ B、x³-a³ C、x³+2a²x+a³ D、x²+2ax²+a³

查看试题解析
6. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 ${(a + b)}^{n} (n$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $a$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 ${(x + 1)}^{2019}$ 展开式中含 $x^{2018}$ 项的系数是 $($ 　　 $)$

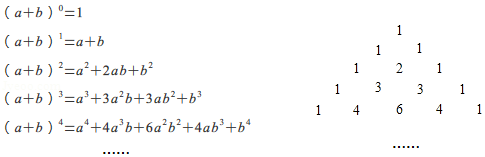A、2016 B、2017 C、2018 D、2019

查看试题解析
7. 如图1的8张宽为a，长为 $b (a < b)$ 的小长方形纸片，按如图2的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示.设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）

A、 $b = 5 a$ B、 $b = 4 a$ C、 $b = 3 a$ D、 $b = a$

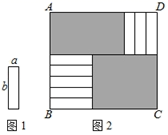查看试题解析
8. 如图，在我国南宋数学家杨辉所著的《详解九章算术》一书中，介绍了(a+b)ⁿ展开式的系数规律，称为“杨辉三角”．如第5行的5个数是1，4，6，4，1，恰好对应着 ${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$ 展开式中的各项系数．利用上述规律计算关于x的多项式 $(3 x^{2} + 2 x + 1) {(x^{2} + 1)}^{5}$ 中 $x^{6}$ 项的系数为（）

A、80 B、60 C、40 D、20

查看试题解析

二、填空题

9. 若 $(x + 3) (x + m) = x^{2} - 2 x - 15$ ．则m＝．

查看试题解析
10. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图一）就是一例．这个三角形给出了（a+b）ⁿ（n＝1，2，3，4，5，6…）的展开式的系数规律．请你仔细观察下表中的规律，按照上述规律，则（a+b）⁶展开式中第二项的系数是；（a+b）⁹⁸展开式中第三项的系数是．

查看试题解析
11. 已知 $(x^{2} + m x + n) (x^{2} - 3 x + 2)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，则 $m + n =$ ．

查看试题解析
12. 如图，正方形卡片A类、B类和长方形卡片C类各若干张（a≠b），如果要选用上述3类卡片共12张拼成一个大长方形（拼接时不可重叠，不可有缝隙）、且卡片全部用上，则不同的选取方案有种．

查看试题解析
13. 用纸片拼图时，我们发现利用图1中的三种纸片（边长分别为 $a$ ， $b$ 的正方形和长为 $b$ 宽为 $a$ 的长方形）各若干，可以拼出一些长方形来解释某些等式，比如图2可以解释为： $(a + 2 b) (a + b) = a^{2} + 3 a b + 2 b^{2}$ ．

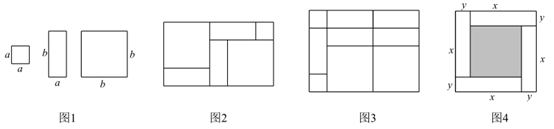(1)、图3可以解释为等式：；

(2)、要拼出一个两边长为 $a + b$ ， $3 a + b$ 的长方形，先回答需要以下三种纸片各多少块，再用画图或整式乘法验证你的结论；
块，块，块

(3)、如图4，大正方形的边长为 $m$ ，小正方形的边长为 $n$ ，若用 $x$ ， $y$ （ $x > y$ ）表示四个相同小长方形的两边长，以下关系式正确的是（填序号）．① $x + y = m$ ；② $2 x y = m^{2} - n^{2}$ ；③ $x^{2} - y^{2} = m n$ ；④ $x^{2} + y^{2} = m^{2} + n^{2}$ ．

查看试题解析

三、解答题

14. 教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：

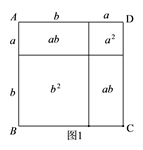
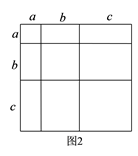
（1）把它看成是一个大正方形，则它的面积为 ${(a + b)}^{2}$ ；
（2）把它看成是2个小长方形和2个小正方形组成的，则它的面积为 $a^{2} + 2 a b + b^{2}$ ；因此，可得到等式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .
① 类比教材中的方法，由图2中的大正方形可得等式：                          .
② 试在图2右边空白处画出面积为 $2 a^{2} + 3 a b + b^{2}$ 的长方形的示意图（标注好a、b），由图形可知，多项式 $2 a^{2} + 3 a b + b^{2}$ 可分解因式为：                          ．
在上方空白处画出②中的示意图
③ 若将代数式 ${(a_{1} + a_{2} + a_{3} + \dots + a_{20})}^{2}$ 展开后合并同类项，得到多项式N，则多项式N的项数一共有                          项.

查看试题解析
15. 数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释 $.$ 如图 $1$ ，有足够多的 $A$ ， $B$ ， $C$ 三种纸片： $A$ 种是边长为 $m$ 的正方形， $B$ 种是边长为 $n$ 的正方形， $C$ 种是宽为 $m$ ，长为 $n$ 的长方形 $.$ 用 $A$ 种纸片 $1$ 张， $B$ 种纸片 $1$ 张， $C$ 种纸片 $2$ 张可以拼出 $($ 不重不漏 $)$ 如图 $2$ 所示的正方形 $.$ 根据正方形的面积，可以用来解释整式乘法 $(m + n) (m + n) = m^{2} + 2 m n + n^{2}$ ，反过来也可以解释多项式 $m^{2} + 2 m n + n^{2}$ ，因式分解的结果为 $m^{2} + 2 m n + n^{2} = (m + n)^{2}$ ，依据上述积累的数与形对应关系的经验，解答下列问题：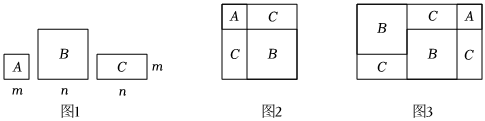

(1)、若多项式 $m^{2} + 2 n^{2} + 3 m n$ 表示分别由 $1$ ， $2$ ， $3$ 张 $A$ ， $B$ ， $C$ 三种纸片拼出如图 $3$ 所示的大长方形的面积，请根据图形求出这个长方形的长和宽，并对多项式 $m^{2} + 3 m n + 2 n^{2}$ 进行因式分解；

(2)、我们可以借助图 $3$ 再拼出一个更大的长方形，使该长方形刚好由 $3$ 张 $A$ 种纸片， $2$ 张 $B$ 种纸片， $7$ 张 $C$ 种纸片拼成，那么这个长方形的面积可以表示为多项式，据此可得到该多项式因式分解的结果为．

查看试题解析

四、综合题

16.

(1)、计算观察下列各式填空：
第1个： $(a - b) (a + b) =$ ；
第2个： $(a - b) (a^{2} + a b + b^{2}) =$ ；
第3个： $(a - b) (a^{3} + a^{2} b + a b^{2} + b^{2}) =$ ；
这些等式反映出多项式乘法的某种运算规律．

(2)、猜想：若n为大于1的正整数，则 $(a - b) (a^{n - 1} + a^{n - 2} b + a^{n - 3} b^{2} + \cdot \cdot \cdot + a^{2} b^{n - 3} + a b^{n - 2} + b^{n - 1}) =$ ．

(3)、利用（2）的猜想结论计算： $2^{n - 1} + 2^{n - 2} + 2^{n - 3} + \cdot \cdot \cdot + 2^{3} + 2^{2} + 2 + 1 =$ ．

(4)、扩展与应用： $3^{n - 1} + 3^{n - 2} + 3^{n - 3} + \cdot \cdot \cdot + 3^{3} + 3^{2} + 3 + 1 =$ ．

查看试题解析
17. 18世纪欧拉引进了求和符号“ $\sum_{k = i}^{n} k$ ”（其中 $i \leq n$ ，且i和n表示正整数），对这个符号我们进行如下定义： $\sum_{k = i}^{n} k$ 表示k从i开始取数一直取到n，全部加起来，即 $\sum_{k = i}^{n} k = i + (i + 1) + (i + 2) + (i + 3) + \cdot \cdot \cdot + n$ ．例如：当i=1时， $\sum_{k = 1}^{n} k = 1 + 2 + 3 + 4 + \cdot \cdot \cdot + n$ ．

(1)、① $\sum_{k = 1}^{9} k$ ， ② $\sum_{k = 9}^{12} k$ ， ③ $\sum_{k = 14}^{16} k$ 中和为45的是；（填写编号）

(2)、 $\sum_{k = 3}^{5} (1 + k) =$ ；

(3)、 $\sum_{k = 3}^{n} (2 - k) =$ ；（用含n的式子表示）

(4)、若 $\sum_{k = 2}^{n} (x - k) (x - k + 1) = 3 x^{2} + p x + m$ ，则 $n =$ ， $p =$ ， $m =$ ．

查看试题解析