2023-2024学年湘教版初中数学七年级下册 2.1.4 多项式的乘法同步分层训练基础题

试卷更新日期：2024-01-26 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 计算 (x−1)(x+2) 的结果是（    ）
    A、x2+x−2 B、x2−x−2 C、x2+2 D、x2−2

    查看试题解析

  • 2. 下列各式中，结果是x2+7x-18的是（ ）
    A、(x-1)(x+18) B、(x+2)(x+9) C、(x-3)(x+6) D、(x-2)(x+9)

    查看试题解析

  • 3. 已知(x+a)(x+b)=x2+cx−8 ， 若a ， b均为整数，则c的值不可能为（    ）
    A、4 B、−2 C、−7 D、7

    查看试题解析

  • 4. 若(x+4)(x−2)=x2+px+q ， 则p、q的值是（    ）
    A、2，−8 B、−2 ， −8 C、−2 ， 8 D、2，8

    查看试题解析

  • 5. 若(3x+1)(-2x+5)=-6x2+mx+n，则m的值为（ ）
    A、3 B、-2 C、13 D、5

    查看试题解析

  • 6. 下列计算错误的是（ ）
    A、(x+a)(x+b)=x2+(a+b)x+ab B、(x+a)(x-b)=x2+(a-b)x+ab C、(x-a)(x+b)=x2-(a-b)x-ab D、(x-a)(x-b)=x2-(a+b)x+ab

    查看试题解析

  • 7. 如果长方形的长为(4a2-2a+1)，宽为(2a+1)，则这个长方形的面积为（ ）
    A、8a3-4a2+2a-1 B、8a3+4a2-2a-1 C、8a3-1 D、8a3+1

    查看试题解析

  • 8. 如果四个互不相同的正整数m，n，p，q满足(6-m)(6-n)(6-p)(6-q)=4，那么m+n+p+q=(　　)

    A、24　　　　 B、25　　　　　 C、26　　　 D、28

    查看试题解析

二、填空题

  • 9. 计算：−4a(a−2b)= ．

    查看试题解析

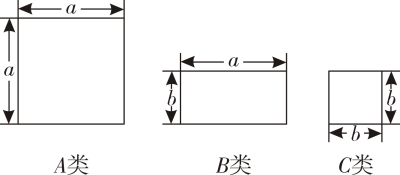
  • 10. 若（x2-x+1）（x-q）的乘积中不含x2项，则q= ．

    查看试题解析

  • 11. 一块三角形铁板余料的底边长是(2a+6b)米，这边上的高是(4a-5b)米，则这块铁板的面积是

    查看试题解析

  • 12. 如图所示的正方形和长方形卡片各有若干张，若要拼成一个长为(2a+b)，宽为(a+ b)的长方形，则需要A类卡片张，B类卡片张，C类卡片张．

    查看试题解析

  • 13. 定义运算：a⊕b=(a+b)(a-3)，下面给出这种运算的四个结论：①4⊕5=9；②a⊕b=b⊕a；③若a⊕b=0，则a+b=0；④若a+b=0，则a⊕b=0．其中正确的结论是(把所有正确结论的序号都填在横线上)

    查看试题解析

三、解答题

  • 14. 一个长方形的长、宽分别为a(cm)，b(cm)， 将长方形的长和宽各增加2cm．
    (1)、新长方形的面积比原长方形的面积增加多少？
    (2)、如果新长方形的面积是原长方形面积的2倍，求(a-2)(b-2)的值．

    查看试题解析

  • 15. 红枣丰收了，为了运输方便，小华的爸爸打算把一个长为(a+2b) cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子，在长方形的四个角各截去一个边长为12 bcm的小正方形，然后沿虚线折起即可，如图所示．

    (1)、现将盒子的外表面贴上彩纸，用代数式表示至少需要多大面积的彩纸；
    (2)、当a=8，b=6时，求所需彩纸的面积．

    查看试题解析

四、综合题

  • 16. 如图，某体育训练基地，有一块长(3a−5b)米，宽(a−b)米的长方形空地，现准备在这块长方形空地上建一个长a米，宽(a−2b)米的长方形游泳池，剩余四周全部修建成休息区.(结果需要化简) 

    (1)、求长方形游泳池面积；
    (2)、求休息区面积；
    (3)、比较休息区与游泳池面积的大小关系．

    查看试题解析

  • 17.
    (1)、计算：

    ①(x+9)(x+4)；

    ②(x−2)(x−18) ．

    (2)、分别求n的值：

    ①(x−3)(x+m)=x2+nx+36；

    ②(x−6)(x+m)=x2+nx+36 ．

    (3)、已知(x+p)(x+q)=x2+nx+6 ， p、q为正整数，求n的值．

    查看试题解析