2023-2024学年湘教版初中数学七年级下册 2.1.1 同底数幂的乘法同步分层训练培优题

试卷更新日期：2024-01-26 类型：同步测试

进入出卷网下载

一、选择题

1. 已知m，n是正整数，且2^m·2ⁿ=2⁵ ，则m，n的值共有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
2. x^3m^＋¹可以写成（）

A、x³·x^(m+1) B、x³＋x^(m+1) C、x·x^3m D、x^m＋x^(2m+1)

查看试题解析
3. 如图，在甲、乙、丙三只袋中分别装有球29个、29个、5个，先从甲袋中取出 $2^{x}$ 个球放入乙袋，再从乙袋中取出 $(2^{x} + 2^{y})$ 个球放入丙袋，最后从丙袋中取出 $2^{y}$ 个球放入甲袋，此时三只袋中球的个数相同，则 $2^{x + y}$ 的值等于（）

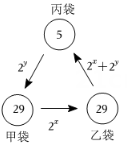A、128 B、64 C、32 D、16

查看试题解析
4. 我们知道，同底数幂的乘法法则为a^m•a^m＝a^m+n（其中a≠0，m、n为正整数），类似地我们规定关于任意正整数m、n的一种新运算：h（m+n）＝h（m）•h（n）；比如h（2）＝3，则h（4）＝h（2+2）＝3×3＝9，若h（2）＝k（k≠0），那么h（2n）·h（2020）的结果是（）

A、2kⁿ⁺²⁰²¹ B、2kⁿ⁺²⁰²² C、kⁿ⁺¹⁰¹⁰ D、2022k

查看试题解析
5. 若 $\underset{2023 个}{\underset{︸}{(2023 \times 2023 \times \dots \times 2023)}} \underset{2023 个}{\underset{︸}{(2023 + 2023 + \dots + 2023)}} = 202 3^{n}$ ，则n为（）

A、2022 B、2023 C、2024 D、2025

查看试题解析
6. 计算 $0 . 5^{22} \times {(- 2)}^{23}$ 的值是（）

A、 $- 0.5$ B、 $0.5$ C、 $- 2$ D、2

查看试题解析
7. 若 $x > 1$ ， $y > 0$ ，且满足 $x y = x^{y} ， \frac{x}{y} = x^{3 y}$ ，则 $x + y$ 的值为（）.

A、1 B、2 C、 $\frac{9}{2}$ D、 $\frac{11}{2}$

查看试题解析
8. 为了求 $1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}$ 的值，可设 $s = 1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}$ ，等式两边同乘以 $2$ ，得 $2 s = 2 (1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}) = 2 + 2^{2} + 2^{3} + \dots + 2^{51}$ ，所以得 $2 s - s = (2 + 2^{2} +$ $2^{3} + \dots + 2^{51}) - (1 + 2 + 2^{2} + 2^{3} + \dots + 2^{50}) = 2^{51} - 1$ ，所以 $s = 2^{51} - 1$ ，即： $1 + 2 + 2^{2} + 2^{3} +$ $\dots + 2^{50}$ ＝ $2^{51} - 1$ .仿照以上方法求 $1 + 5 + 5^{2} + 5^{3} + \dots + 5^{2020}$ 的值为（）

A、 $5^{2021} - 1$ B、 $5^{2020} - 1$ C、 $\frac{5^{2020} - 1}{4}$ D、 $\frac{5^{2021} - 1}{4}$

查看试题解析

二、填空题

9. 若7^-2×7^-1×7⁰=7^P ，则p的值为

查看试题解析
10. 若 $a^{n} = b (a > 0$ 且 $a \neq 1$ ， $b > 0)$ ，则 $n$ 叫做以 $a$ 为底 $b$ 的对数，记为 $l o g_{a}$ $b$ （即 $l o g_{a}$ $b = n)$ ，如 $3^{4} = 81$ ，则4叫做以3为底81的对数，记为 $l o g_{3} 81$ （即 $l o g_{3} 81 = 4)$ ．则 $l o g_{2} 64$ 的值为．

查看试题解析
11. 如果 $a^{c} = b$ ，那么我们规定 $(a ， b) = c$ ．例如，因为 $2^{3} = 8$ ，所以 $(2 ， 8) = 3$ ．

(1)、根据上述规定填空： $(4 ， 1) =$ ；

(2)、记 $(3 ， 5) = a$ ， $(3 ， 6) = b$ ， $(3 ， 30) = c$ ，则 $a$ ， $b$ ， $c$ 之间的等量关系．

查看试题解析
12. 若a^m=2，aⁿ=3，则a^m+n等于

查看试题解析
13. 已知2^a＝5，2^b＝10，2^c＝100，那么a、b、c之间满足的等量关系是．

查看试题解析

三、解答题

14. 数学课上老师与同学们一起利用球的体积公式 $V = \frac{4}{3} π r^{3}$ 计算出地球的体积约是 $1.08 \times 1 0^{12}$ 立方千米，接着老师问道：“科学家们正在寻找一颗星球，也可以近似地看做球体，它的半径是地球的10000倍，那么这样的星球它的体积约是多少立方千米？”请你尝试计算.

查看试题解析
15. 用字母表示同底数幂的乘法法则，并写出推导过程及每一步的依据．

查看试题解析

四、综合题

16. 规定新运算“☆”：a☆b=10^a×10^b.例如，3☆4=10³×10⁴=10⁷。

(1)、试求2☆5和3☆17的值；

(2)、猜想：a☆b与b☆a的运算结果是否相等？说明理由。

查看试题解析
17. 先阅读下列材料，然后解答问题.
探究：用的幂的形式表示a^m•a^_n的结果（m、为正整数）.

分析：根据乘方的意义，a^m•aⁿ= $\overset{m 个}{\overset{︷}{a \cdot a \cdot a \cdot ⋯ \cdot a}} \cdot \overset{n 个}{\overset{︷}{a \cdot a \cdot a \cdot ⋯ \cdot a}} = \overset{(m + n) 个}{\overset{︷}{a \cdot a \cdot a \cdot ⋯ \cdot a}}$ =a^m+n.

(1)、请根据以上结论填空：3⁶×3⁸= ，5²×5³×5⁷= ，（a+b）³•（a+b）⁵= ；

(2)、仿照以上的分析过程，用的幂的形式表示（a^m）ⁿ的结果（提示：将a^m看成一个整体）.

查看试题解析